안녕하세요. 지난 포스팅의 디지털 영상 처리 - 노이즈 모델에서는 디지털 영상에 부가되는 다양한 노이즈들에 대해서 알아보았습니다. 오늘은 영상에 노이즈를 부가하는 방법에 대해서 알아보겠습니다. 전체 코드는 아래의 깃허브를 참조해주시길 바랍니다.
skawngus1111/DIP
Digital Image Processing exercise&code. Contribute to skawngus1111/DIP development by creating an account on GitHub.
github.com
일단... 샘플링하는 방법을 통째로 구현해보려고 했지만 제 코딩실력의 한계로 이 부분은 아래의 MathWorks 파일을 이용했다는 점 참고해주시길 바랍니다. 해당 코드에는 약 50가지의 다양한 분포에 대한 샘플링을 할 수 있는 코드이기 때문에 앞으로 저희에게 큰 도움이 될 거 같습니다.
RANDRAW
Efficient Random Variates Generator (from over 50 distributions).
kr.mathworks.com
샘플링만 한다면 영상에 노이즈를 부가하는 것은 간단하기 때문에 실제로 위 함수를 이용해서 샘플링이 잘 되는 지 알아보기 위해서 5십만개의 샘플을 뽑아서 히스토그램으로 그려보도록 하겠습니다.
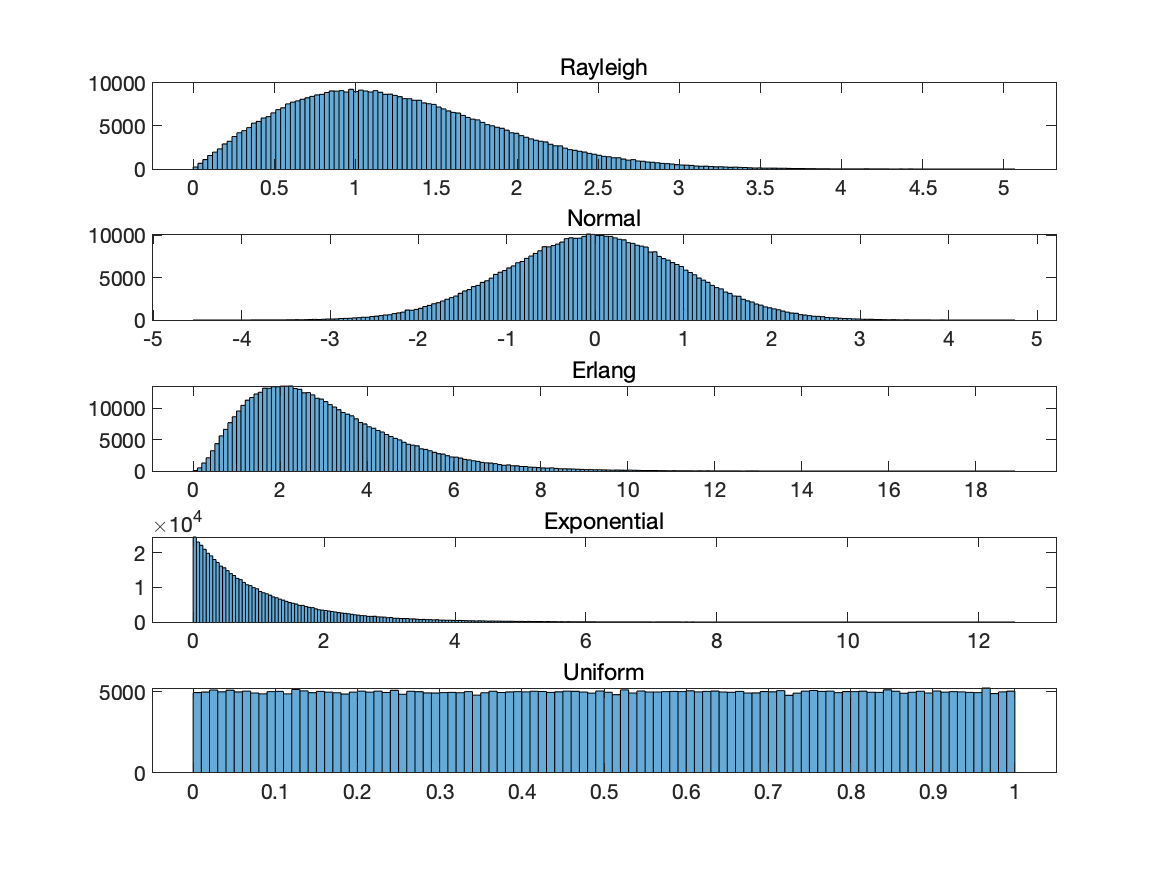
확실히 저희가 지난 포스팅에서 보았던 분포와 유사한 그림을 보이고 있습니다. 잘 되는 거 같으니 바로 영상에 노이즈를 부가해보도록 하겠습니다. 영상에 노이즈를 추가하는 방법은 영상의 크기와 동일하게 노이즈를 샘플링한 뒤 더하는 것이 끝입니다!! 아주 간단하죠? 임의의 영상 $f(x, y)$에 대해서 노이즈 $\eta(x, y)$를 부가한다는 것을 수식으로 표현하면 아래와 같이 모델링할 수 있습니다.
$$\hat{f}(x, y) = f(x, y) + \eta(x, y)$$
여기서 $\eta(x, y)$는 영상 $f(x, y)$와 크기가 동일하고 위에 나온 정규 분포, 레일리 분포, 일랑, 지수, 균등 분포 중 한 가지가 될 수 있습니다. 예를 들어 정규분포를 따르는 노이즈, 즉 가우시안 분포를 적용하면 아래와 같이 나오게 됩니다.

이때, 정규 분포의 분산이 커질수록 노이즈가 아주 심해지는 것을 관찰할 수 있습니다. 분산이 5가 되니 아예 기존의 영상을 알아볼 수가 없어졌네요.
'image processing' 카테고리의 다른 글
| 디지털 영상 처리 - 노이즈만 있을 때 복원하기(공간 필터링) : 적응 필터 (0) | 2021.05.12 |
|---|---|
| 디지털 영상 처리 - 노이즈만 있을 때 복원하기(공간 필터링) : 평균 필터와 순서-통계 필터 (1) | 2021.05.10 |
| 디지털 영상 처리 - 노이즈 모델들 (0) | 2021.05.05 |
| 디지털 영상 처리 - 영상 열화 및 복원 과정 모델 (0) | 2021.05.02 |
| 디지털 영상 처리 - 선택적 필터링 (0) | 2021.04.28 |
안녕하세요. 지난 포스팅의 디지털 영상 처리 - 노이즈 모델에서는 디지털 영상에 부가되는 다양한 노이즈들에 대해서 알아보았습니다. 오늘은 영상에 노이즈를 부가하는 방법에 대해서 알아보겠습니다. 전체 코드는 아래의 깃허브를 참조해주시길 바랍니다.
skawngus1111/DIP
Digital Image Processing exercise&code. Contribute to skawngus1111/DIP development by creating an account on GitHub.
github.com
일단... 샘플링하는 방법을 통째로 구현해보려고 했지만 제 코딩실력의 한계로 이 부분은 아래의 MathWorks 파일을 이용했다는 점 참고해주시길 바랍니다. 해당 코드에는 약 50가지의 다양한 분포에 대한 샘플링을 할 수 있는 코드이기 때문에 앞으로 저희에게 큰 도움이 될 거 같습니다.
RANDRAW
Efficient Random Variates Generator (from over 50 distributions).
kr.mathworks.com
샘플링만 한다면 영상에 노이즈를 부가하는 것은 간단하기 때문에 실제로 위 함수를 이용해서 샘플링이 잘 되는 지 알아보기 위해서 5십만개의 샘플을 뽑아서 히스토그램으로 그려보도록 하겠습니다.

확실히 저희가 지난 포스팅에서 보았던 분포와 유사한 그림을 보이고 있습니다. 잘 되는 거 같으니 바로 영상에 노이즈를 부가해보도록 하겠습니다. 영상에 노이즈를 추가하는 방법은 영상의 크기와 동일하게 노이즈를 샘플링한 뒤 더하는 것이 끝입니다!! 아주 간단하죠? 임의의 영상 $f(x, y)$에 대해서 노이즈 $\eta(x, y)$를 부가한다는 것을 수식으로 표현하면 아래와 같이 모델링할 수 있습니다.
$$\hat{f}(x, y) = f(x, y) + \eta(x, y)$$
여기서 $\eta(x, y)$는 영상 $f(x, y)$와 크기가 동일하고 위에 나온 정규 분포, 레일리 분포, 일랑, 지수, 균등 분포 중 한 가지가 될 수 있습니다. 예를 들어 정규분포를 따르는 노이즈, 즉 가우시안 분포를 적용하면 아래와 같이 나오게 됩니다.

이때, 정규 분포의 분산이 커질수록 노이즈가 아주 심해지는 것을 관찰할 수 있습니다. 분산이 5가 되니 아예 기존의 영상을 알아볼 수가 없어졌네요.
'image processing' 카테고리의 다른 글
| 디지털 영상 처리 - 노이즈만 있을 때 복원하기(공간 필터링) : 적응 필터 (0) | 2021.05.12 |
|---|---|
| 디지털 영상 처리 - 노이즈만 있을 때 복원하기(공간 필터링) : 평균 필터와 순서-통계 필터 (1) | 2021.05.10 |
| 디지털 영상 처리 - 노이즈 모델들 (0) | 2021.05.05 |
| 디지털 영상 처리 - 영상 열화 및 복원 과정 모델 (0) | 2021.05.02 |
| 디지털 영상 처리 - 선택적 필터링 (0) | 2021.04.28 |
