안녕하세요. 지난 포스팅의 디지털 영상 처리 - 영상 열화 및 복원 과정 모델에서는 영상이 부가 노이즈 $\eta{x, y}$나 열화 함수 $h(x, y)$에 의해 오염되는 과정에 대해서 알아보았습니다. 오늘은 그중에서 부가 노이즈 $\eta(x, y)$에는 어떤 종류들이 있는 지 알아보도록 하겠습니다.
본격적으로 진행하기 전에 백색 노이즈(White noise)라는 말 들어보셨나요? 제가 어렸을 때는 홈 쇼핑으로 백색 노이즈 생성해주는 기계를 옆에 두고 공부하면 더 집중이 잘된다는 상품 홍보 영상을 본적이 있습니다. 아니면 최근 유튜브에 많은 ASMR 영상에서도 종종 등장하는 용어입니다. 저희는 현재 디지털 영상 처리를 배우고 있기 때문에 이를 영상으로 확장시켜서 정의해보면 백색 노이즈란 노이즈를 주파수 도메인으로 변환시켰을 때 스펙트럼이 전부 상수인 경우를 의미합니다.
그리고 오늘 설명할 노이즈 모델들에 대해서 노이즈가 공간 좌표와 무관하고 영상 자체와 어떠한 관련성도 없다고 가정하겠습니다. 이러한 가정은 부분적으로는 유효하지 않겠지만 공간에 종속적이고 상관성이 존재하는 노이즈를 다루는 것은 아직 저희에게는 벅차기 때문에 유용한 가정이라고 생각해주시면 감사하겠습니다.
1. 중요한 노이즈 모델들
앞으로 설명드릴 노이즈 모델들의 특성들은 노이즈가 따르고 있는 아래의 그림과 같은 확률 밀도 분포(Probability Density Distribution; PDF)에 따라서 달라집니다.

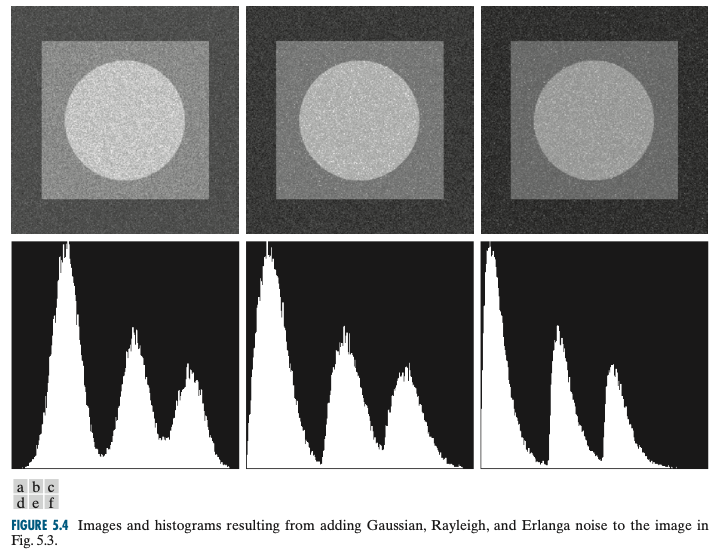
가우시안 노이즈(Gaussian Noise)
이제는 놀랍지도 않습니다. 가우스 관련 용어가 또 나와버렸네요. 역시 수학 뿐만 아니라 디지털 영상 처리 세계관 최강자답습니다. 가우시안 노이즈의 PDF는 아래와 같습니다.
$$p(z) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(z - \bar{z})^{2}}{2\sigma^{2}}}$$
가우시안은 자연 현상에서 가장 자주 보이는 노이즈 중에 하나이기 때문에 노이즈에 대한 정보가 하나도 없다면 보통 가우시안 노이즈라고 가정하는 편입니다.
Rayleigh 노이즈(Rayleigh Noise)
Rayleigh 노이즈의 PDF를 보면 가우시안 PDF에 비해 원점과 가깝고 왼쪽으로 살짝 치우쳐있는 것을 관찰할 수 있습니다. 이와 같은 형태의 PDF는 휘어진 히스토그램을 근사화하는 데 유용하게 사용될 수 있으며 PDF는 아래와 같습니다.
$$p(z) = \begin{cases} \frac{2}{b}(z - a)e^{-\frac{(z -a)^{2}}{b}} &z \ge a \\ 0 & z < a\end{cases}$$
이때, Rayleigh 노이즈 PDF의 평균과 분산은 다음으로 얻을 수 있습니다.
$$\bar{z} = a + \sqrt{\frac{\pi b}{4}}$$
$$\sigma^{2} = \frac{b(4 - \pi)}{4}$$
Erlang 노이즈(Erlang Noise)
Erlang 노이즈의 PDF는 아래와 같이 주어집니다.
$$p(z) = \begin{cases} \frac{a^{b}z^{b - 1}}{(b - 1)!}e^{-az} &z \ge 0 \\ 0 &z < 0 \end{cases}$$
여기서 각 파라미터는 $a > 0$, $b$는 양의 정수를 의미합니다. 그리고 $!$는 계승(factorial)을 의미하죠. 그리고 이 PDF의 평균과 분산은 아래와 같습니다.
$$\bar{z} = \frac{b}{a}$$
$$\sigma^{2} = \frac{b}{a^{2}}$$
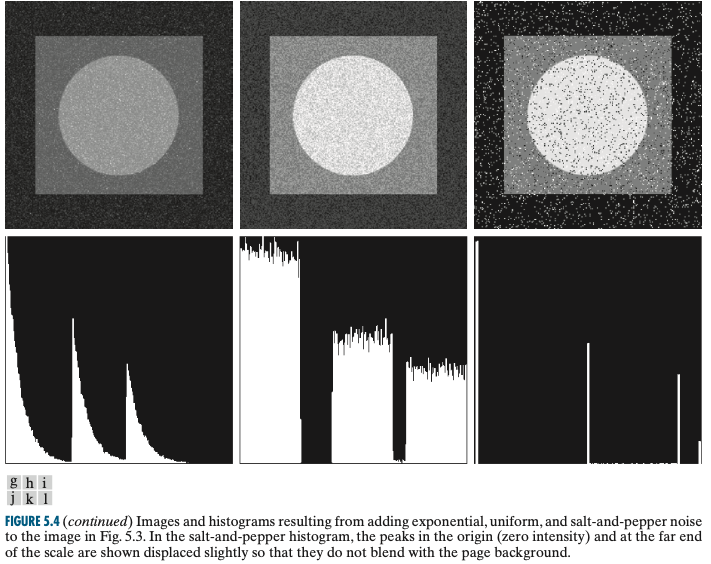
지수 노이즈(Exponential Noise)
지수 노이즈의 PDF는 여러분도 잘 아시다싶이 아래와 같이 주어집니다.
$$p(z) = \begin{cases}ae^{-az} &z \ge 0 \\ 0 &z < 0 \end{cases}$$
여기서 $a > 0$이여야합니다. 그리고 이 PDF의 평균과 분산은 아래와 같습니다.
$$\bar{z} = \frac{1}{a}$$
$$\sigma^{2} = \frac{1}{a^{2}}$$
이때, 지수 노이즈는 Erlang 노이즈의 특별한 형태입니다. Erlang 노이즈에서 $b = 1$로 바꾸면 지수 노이즈가 됨을 쉽게 알 수 있습니다.
균등 노이즈(Uniform Noise)
균등 노이즈의 PDF도 다들 잘 아실겁니다.
$$p(z) = \begin{cases} \frac{1}{b - a} &a \le z \le b \\ 0 &\text{Otherwise} \end{cases}$$
그리고 이 PDF의 평군과 분산은 아래와 같습니다.
$$\bar{z} = \frac{a + b}{2}$$
$$\sigma^{2} = \frac{(b - a)^{2}}{12}$$
소금-후추 노이즈(Salt-Pepper Noise)
소금-후추 노이즈의 PDF는 아래와 같이 주어집니다.
$$p(z) = \begin{cases} P_{a} &z = a \\ P_{b} &z = b \\ 1 - P_{a} - P_{b} &\text{Otherwise} \end{cases}$$
이러한 노이즈들을 추가했을 때 영상의 히스토그램을 분석해보면 추가된 노이즈마다 특성이 존재하게 됩니다.
2. 주기가 존재하는 노이즈(Periodic Noise)
혹시 주파수 공간에서의 필터링에서 노치 필터를 이용해서 반복적인 패턴을 가진 노이즈를 제거하는 방법이 기억나시나요? 이러한 반복적인 패턴의 노이즈는 보통 영상 획득 동안에 전기적 또는 전기 기계 간 간섭에 의해 발생하는 경우가 많습니다. 이번에 설명하는 주기적인 특성이 존재하는 노이즈만큼은 공간에 종속적이라고 가정하도록 하겠습니다. 지난 포스팅에서도 설명드렸지만 노치 필터를 이용하면 아러한 주기적 노이즈를 상당히 많이 제거 가능합니다. 왜냐하면 주기적 특성을 가지는 노이즈들은 보통 주파수 도메인에서 아래와 같이 구별하기 쉽기 때문이죠.

'image processing' 카테고리의 다른 글
| 디지털 영상 처리 - 노이즈만 있을 때 복원하기(공간 필터링) : 평균 필터와 순서-통계 필터 (1) | 2021.05.10 |
|---|---|
| 디지털 영상 처리 - 노이즈 모델 구현 (0) | 2021.05.07 |
| 디지털 영상 처리 - 영상 열화 및 복원 과정 모델 (0) | 2021.05.02 |
| 디지털 영상 처리 - 선택적 필터링 (0) | 2021.04.28 |
| 디지털 영상 처리 - 주파수 도메인 필터를 이용한 영상 샤프닝 구현 (0) | 2021.04.26 |
안녕하세요. 지난 포스팅의 디지털 영상 처리 - 영상 열화 및 복원 과정 모델에서는 영상이 부가 노이즈 $\eta{x, y}$나 열화 함수 $h(x, y)$에 의해 오염되는 과정에 대해서 알아보았습니다. 오늘은 그중에서 부가 노이즈 $\eta(x, y)$에는 어떤 종류들이 있는 지 알아보도록 하겠습니다.
본격적으로 진행하기 전에 백색 노이즈(White noise)라는 말 들어보셨나요? 제가 어렸을 때는 홈 쇼핑으로 백색 노이즈 생성해주는 기계를 옆에 두고 공부하면 더 집중이 잘된다는 상품 홍보 영상을 본적이 있습니다. 아니면 최근 유튜브에 많은 ASMR 영상에서도 종종 등장하는 용어입니다. 저희는 현재 디지털 영상 처리를 배우고 있기 때문에 이를 영상으로 확장시켜서 정의해보면 백색 노이즈란 노이즈를 주파수 도메인으로 변환시켰을 때 스펙트럼이 전부 상수인 경우를 의미합니다.
그리고 오늘 설명할 노이즈 모델들에 대해서 노이즈가 공간 좌표와 무관하고 영상 자체와 어떠한 관련성도 없다고 가정하겠습니다. 이러한 가정은 부분적으로는 유효하지 않겠지만 공간에 종속적이고 상관성이 존재하는 노이즈를 다루는 것은 아직 저희에게는 벅차기 때문에 유용한 가정이라고 생각해주시면 감사하겠습니다.
1. 중요한 노이즈 모델들
앞으로 설명드릴 노이즈 모델들의 특성들은 노이즈가 따르고 있는 아래의 그림과 같은 확률 밀도 분포(Probability Density Distribution; PDF)에 따라서 달라집니다.

가우시안 노이즈(Gaussian Noise)
이제는 놀랍지도 않습니다. 가우스 관련 용어가 또 나와버렸네요. 역시 수학 뿐만 아니라 디지털 영상 처리 세계관 최강자답습니다. 가우시안 노이즈의 PDF는 아래와 같습니다.
$$p(z) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(z - \bar{z})^{2}}{2\sigma^{2}}}$$
가우시안은 자연 현상에서 가장 자주 보이는 노이즈 중에 하나이기 때문에 노이즈에 대한 정보가 하나도 없다면 보통 가우시안 노이즈라고 가정하는 편입니다.
Rayleigh 노이즈(Rayleigh Noise)
Rayleigh 노이즈의 PDF를 보면 가우시안 PDF에 비해 원점과 가깝고 왼쪽으로 살짝 치우쳐있는 것을 관찰할 수 있습니다. 이와 같은 형태의 PDF는 휘어진 히스토그램을 근사화하는 데 유용하게 사용될 수 있으며 PDF는 아래와 같습니다.
$$p(z) = \begin{cases} \frac{2}{b}(z - a)e^{-\frac{(z -a)^{2}}{b}} &z \ge a \\ 0 & z < a\end{cases}$$
이때, Rayleigh 노이즈 PDF의 평균과 분산은 다음으로 얻을 수 있습니다.
$$\bar{z} = a + \sqrt{\frac{\pi b}{4}}$$
$$\sigma^{2} = \frac{b(4 - \pi)}{4}$$
Erlang 노이즈(Erlang Noise)
Erlang 노이즈의 PDF는 아래와 같이 주어집니다.
$$p(z) = \begin{cases} \frac{a^{b}z^{b - 1}}{(b - 1)!}e^{-az} &z \ge 0 \\ 0 &z < 0 \end{cases}$$
여기서 각 파라미터는 $a > 0$, $b$는 양의 정수를 의미합니다. 그리고 $!$는 계승(factorial)을 의미하죠. 그리고 이 PDF의 평균과 분산은 아래와 같습니다.
$$\bar{z} = \frac{b}{a}$$
$$\sigma^{2} = \frac{b}{a^{2}}$$
지수 노이즈(Exponential Noise)
지수 노이즈의 PDF는 여러분도 잘 아시다싶이 아래와 같이 주어집니다.
$$p(z) = \begin{cases}ae^{-az} &z \ge 0 \\ 0 &z < 0 \end{cases}$$
여기서 $a > 0$이여야합니다. 그리고 이 PDF의 평균과 분산은 아래와 같습니다.
$$\bar{z} = \frac{1}{a}$$
$$\sigma^{2} = \frac{1}{a^{2}}$$
이때, 지수 노이즈는 Erlang 노이즈의 특별한 형태입니다. Erlang 노이즈에서 $b = 1$로 바꾸면 지수 노이즈가 됨을 쉽게 알 수 있습니다.
균등 노이즈(Uniform Noise)
균등 노이즈의 PDF도 다들 잘 아실겁니다.
$$p(z) = \begin{cases} \frac{1}{b - a} &a \le z \le b \\ 0 &\text{Otherwise} \end{cases}$$
그리고 이 PDF의 평군과 분산은 아래와 같습니다.
$$\bar{z} = \frac{a + b}{2}$$
$$\sigma^{2} = \frac{(b - a)^{2}}{12}$$
소금-후추 노이즈(Salt-Pepper Noise)
소금-후추 노이즈의 PDF는 아래와 같이 주어집니다.
$$p(z) = \begin{cases} P_{a} &z = a \\ P_{b} &z = b \\ 1 - P_{a} - P_{b} &\text{Otherwise} \end{cases}$$
이러한 노이즈들을 추가했을 때 영상의 히스토그램을 분석해보면 추가된 노이즈마다 특성이 존재하게 됩니다.


2. 주기가 존재하는 노이즈(Periodic Noise)
혹시 주파수 공간에서의 필터링에서 노치 필터를 이용해서 반복적인 패턴을 가진 노이즈를 제거하는 방법이 기억나시나요? 이러한 반복적인 패턴의 노이즈는 보통 영상 획득 동안에 전기적 또는 전기 기계 간 간섭에 의해 발생하는 경우가 많습니다. 이번에 설명하는 주기적인 특성이 존재하는 노이즈만큼은 공간에 종속적이라고 가정하도록 하겠습니다. 지난 포스팅에서도 설명드렸지만 노치 필터를 이용하면 아러한 주기적 노이즈를 상당히 많이 제거 가능합니다. 왜냐하면 주기적 특성을 가지는 노이즈들은 보통 주파수 도메인에서 아래와 같이 구별하기 쉽기 때문이죠.

'image processing' 카테고리의 다른 글
| 디지털 영상 처리 - 노이즈만 있을 때 복원하기(공간 필터링) : 평균 필터와 순서-통계 필터 (1) | 2021.05.10 |
|---|---|
| 디지털 영상 처리 - 노이즈 모델 구현 (0) | 2021.05.07 |
| 디지털 영상 처리 - 영상 열화 및 복원 과정 모델 (0) | 2021.05.02 |
| 디지털 영상 처리 - 선택적 필터링 (0) | 2021.04.28 |
| 디지털 영상 처리 - 주파수 도메인 필터를 이용한 영상 샤프닝 구현 (0) | 2021.04.26 |
