안녕하세요. 지난 포스팅의 디지털 영상 처리 - 주파수 공간 필터링 기초 1에서는 복소수(Complex numbers), 푸리에 급수(Fourier Series), 임펄스(Impulse), 선별 특성(Sifting Property)에 대해서 알아보았습니다. 오늘은 나머지 개념들을 정리해보는 시간을 가지도록 하겠습니다.
1. 푸리에 변환(Fourier Transform)
연속 변수 $t$의 연속 함수 $f(t)$에 대한 푸리에 변환 $\mathcal{F}\{f(t)\}$은 아래와 같이 정의됩니다.
$$\mathcal{F}\{f(t)\} = \int_{-\infty}^{\infty} f(t)e^{-j2\pi\mu t} \; dt$$
위의 정의를 보면 변환과정에서 연속 변수 $t$는 적분 되어 없어지고 새로운 연속 변수 $\mu$가 생기게 됩니다. 따라서 $\mathcal{F}\{f(t)\} = F(\mu)$라고 쓰기도 합니다. 이렇게 변환된 $F(\mu)$가 정의된 공간을 주파수 공간(Frequency Domain)이라고 표현합니다. 이때, 연속 변수 $\mu$를 없애고 연속 변수 $t$를 다시 얻는 역 푸리에 변환(Inverse Fourier Transform)도 정의됩니다.
$$\mathcal{F}^{-1}\{F(\mu)\} = \int_{-\infty}^{\infty} F(\mu)e^{j2\pi\mu t} \; d\mu$$
푸리에 변환과 역푸리에 변환에서 수식의 차이점은 $f(t)$ 대신 $F(\mu)$가 들어가고 지수가 음수에서 양수로 변한다는 점 밖에 없으니 푸리에 변환만 기억해놓으시면 역 푸리에 변환도 쉽게 기억할 수 있습니다.
다른 표기법은 지난 포스티에서도 보았던 오일러 공식(Euler's Formula) $e^{j\theta} = \sin{\theta} + j\cos{\theta}$를 이용하여 아래와 같이 표현할 수 있습니다.
$$\mathcal{F}\{f(t)\} = \int_{-\infty}^{\infty} f(t)\left[\cos{\left(2\pi\mu t\right)} - j\sin{\left(2\pi\mu t\right)}\right] \; dt$$
$$\mathcal{F}^{-1}\{F(\mu)\} = \int_{-\infty}^{\infty} F(\mu)\left[\cos{\left(2\pi\mu t\right)} + j\sin{\left(2\pi\mu t\right)}\right] \; d\mu$$
그렇다면 실제로 간단한 함수를 이용해서 푸리에 변환을 적용해보도록 하겠습니다. 자세한 과정을 보고 싶으신 분은 "더보기"를 눌러주세요.
$$f(t) = \begin{cases} A &-\frac{W}{2} \le t \le \frac{W}{2} \\ 0 &\text{Otherwise}\end{cases}$$
$$F(\mu) = \int_{-\infty}^{\infty} f(t)e^{-j2\pi\mu t} \; dt = \int_{-\frac{W}{2}}^{\frac{W}{2}} Ae^{-j2\pi\mu t} \; dt$$
$$ = -\frac{A}{j2\pi\mu}\left[e^{-j2\pi\mu}\right]_{-\frac{W}{2}}^{\frac{W}{2}} = \frac{-A}{j2\pi\mu}\left[e^{-j\pi\mu W} - e^{j\pi\mu W}\right]$$
$$ = \frac{A}{j2\pi\mu}\left[e^{j\pi\mu W} - e^{-j\pi\mu W}\right]$$
$$ = AW\frac{\sin{\left(\pi\mu W\right)}}{\pi\mu W}$$
$$ = AW\text{sinc}{\left(\mu W\right)}$$
최종 결과는 아래와 같습니다.
$$F(\mu) = AW\text{sinc}{\left(\mu W\right)} = AW\frac{\sin{\left(\pi\mu W\right)}}{\pi\mu W}$$
여기서 $\text{sinc}(m) = \frac{\sin{\pi m}}{\pi m}$으로 정의됩니다. $F(\mu)$를 시각화하면 아래의 그림을 얻을 수 있습니다.
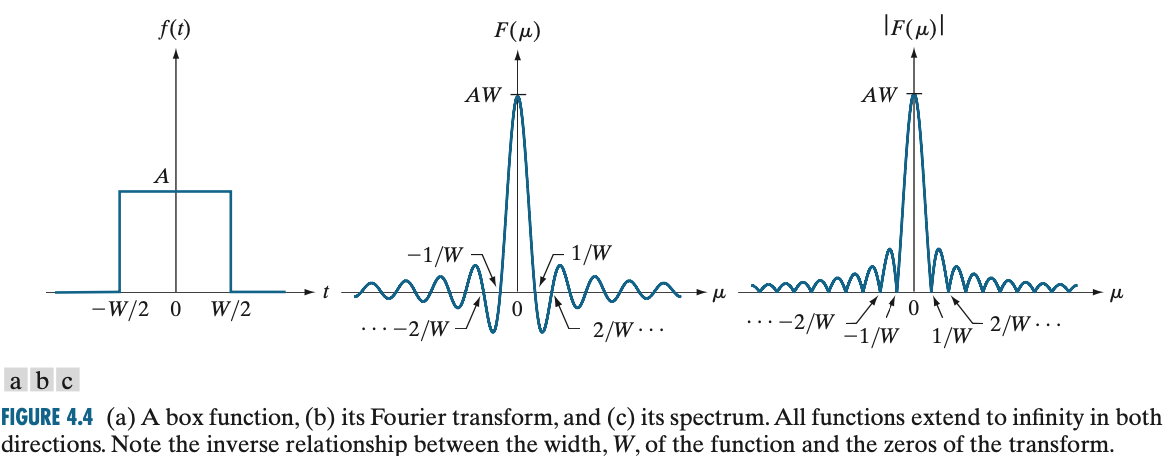
이번 예제의 경우에는 운이 좋게도 남아있지 않지만 일반적으로 푸리에 변환을 하게 되면 복소수항이 남아있게 됩니다. 시각화하기 위해서는 복소수항을 제거해야 하기 때문에 보통 $\left|F(\mu)\right|$를 시각화합니다. 이를 푸리에 스펙트럼(Fourier Spectrum)이라고 합니다.
2. 컨볼루션(Convolution)
영상 공간 필터링에 대해서 소개할 때 컨볼루션 연산에 대해서 코릴레이션과 비교하면서 간단하게 언급하였습니다. 그중에서도 컨볼루션은 주파수 공간 필터링과 영상 공간 필터링 사이의 관계를 만들어주는 아주 중요한 연산이기 때문에 따로 설명을 더 하도록 하겠습니다. 이전에 보았던 컨볼루션은 이산 데이터 간의 연산이었습니다. 하지만 이번에는 연속 함수 간의 연산으로 적용해야 하기 때문에 적분을 이용해서 아래와 같이 정의해주어야 합니다.
$$f(t) * h(t) = \int_{-\infty}^{\infty} f(\tau)h(t - \tau) \; d\tau$$
여기서 음수 부호는 컨볼루션 시 적용하는 윈도우 반전, $t$는 다른 함수를 지나 한 함수를 슬라이딩시키는데 필요한 변위, $\tau$는 적분에 사용되는 부가 변수가 됩니다. 이때, 편의를 위해서 두 함수 $f(t), h(t)$가 $-\infty ~ \infty$에서 정의된다고 가정하겠습니다.
이때, 저희가 관심 있는 것은 두 함수의 컨볼루션의 푸리에 변환, 즉 $\mathcal{F}\{f(t) * h(t)\}$입니다. 실제로 푸리에 변환 공식에 넣어서 계산해보도록 하겠습니다.
$$\mathcal{F}\{f(t) * h(t)\} = \int_{-\infty}^{\infty} \left(f(t) * h(t)\right)e^{-j2\pi\mu t} \; dt$$
$$ = \int_{-\infty}^{\infty} \left[\int_{-\infty}^{\infty} f(\tau)h(t - \tau) \; d\tau\right]e^{-j2\pi\mu t} \; dt $$
$$ = \int_{-\infty}^{\infty} f(\tau)\left[h(t - \tau)e^{-j2\pi\mu t} \; dt\right]d\tau$$
위 식을 자세히 보시면 대괄호의 항은 $h(t - \tau)$의 푸리에 변환입니다. 이후에 증명하겠지만 지금은 $\mathcal{F}\{h(t - \tau)\} = H(\mu)e^{-j2\pi\mu\tau}$임을 받아들이면 다시 정리할 수 있습니다.
$$\mathcal{F}\{f(t) * h(t)\} = \int_{-\infty}^{\infty} f(\tau)\left[h(t - \tau)e^{-j2\pi\mu t} \; dt\right]d\tau$$
$$ = \int_{-\infty}^{\infty} f(\tau)\left[H(\mu)e^{-j2\pi\mu\tau}\right] \; d\tau$$
$$ = H(\mu)\int_{-\infty}^{\infty} f(\tau)e^{-j2\pi\mu\tau} \; d\tau$$
$$ = H(\mu)F(\mu)$$
위의 결과는 저희에게 아주 중요한 성질을 전해줍니다. 영상 공간에서의 컨볼루션 연산은 주파수 공간에서 두 함수의 푸리에 변환의 단순 곱과 같다는 것이죠. 역 푸리에 변환을 이용해면 주파수 공간에서의 컨볼루션 연산은 영상 공간에서 두 함수의 역푸리에 변환의 단순 곱과 같다는 것 역시 증명할 수 있습니다. 이를 "컨볼루션 정리(Convolution Theorem)"이라고 부르며 주파수 공간 필터링의 기본 토대가 됩니다. 다시 정리하면 아래와 같이 쓸 수 있습니다.
$$f(t) * h(t) \leftrightarrow F(\mu)H(\mu)$$
$$f(t)h(t) \leftrightarrow F(\mu) * H(\mu)$$
'image processing' 카테고리의 다른 글
| 디지털 영상 처리 - 샘플링 정리와 샘플링된 함수 복원 (0) | 2021.04.04 |
|---|---|
| 디지털 영상 처리 - 샘플링과 샘플링된 함수의 푸리에 변환 (6) | 2021.03.31 |
| 디지털 영상 처리 - 주파수 공간 필터링 기초 1 (3) | 2021.03.27 |
| 디지털 영상 처리 - 공간 개선 방법 결합 (0) | 2021.03.24 |
| 디지털 영상 처리 - 샤프닝 공간 필터 구현 (0) | 2021.03.22 |
