안녕하세요. 지난 포스팅의 디지털 영상 처리 - 샘플링과 샘플링된 함수의 푸리에 변환에서는 샘플링을 수학적으로 모델링하고 샘플링된 함수에 푸리에 변환을 적용한 결과에 대해서 알아보고 분석해보았습니다. 이를 통해 저희는 아래의 수식을 얻을 수 있었습니다.
$$\tilde{F}(\mu) = \mathcal{F}\{\tilde{f}(t)\} = \frac{1}{\Delta T}\sum_{n = -\infty}^{\infty} F(\mu - \frac{n}{\Delta T})$$
위의 결과는 저희에게 아래의 3가지를 알려주게 됩니다.
- 기존 함수 $f(t)$의 푸리에 변환인 $F(\mu)$라는 함수가 주기 $\frac{1}{\Delta T}$에 의존하여 무한 번 반복된다.
- $\tilde{F}(\mu)$의 반복 주기는 임펄스 열의 주기 $\Delta T$에 반비례한다.
- $\tilde{f}(t)$는 이산함수이지만 $\tilde{F}(\mu)$는 연속함수이다.
여기에 한 걸음 나아가서 샘플링 속도 $\Delta T$를 어떻게 정하느냐에 따라서 샘플링된 함수의 푸리에 변환의 모양이 아래와 같이 변하게 될 것입니다.

샘플링 속도 $\Delta T$를 좁게 잡으면 $\frac{1}{\Delta T}$는 늘어나게 되어 $F(\mu)$끼리 영향을 주지 않는 오버-샘플링(over-sampling) 결과 (a)를 얻게 됩니다. 그에 반해, 샘플링 속도 $\Delta T$를 크게 잡으면 $\frac{1}{\Delta T}$는 줄어들게 되고 이는 $F(\mu)$끼리 서로 영향을 주게 되는 언더-샘플링(under-sampling) 결과 (c)를 얻게 됩니다. 오버-샘플링과 언더-샘플링 사이에서 균형 있는 샘플링 속도 $\Delta T$를 찾으면 이를 임계 샘플링(critical sampling)이라고 합니다.
이와 같은 아이디어를 기반으로 샘플링된 함수로부터 저희가 샘플링되기 전의 함수로 복원할 수 있는 방법을 찾아보도록 하겠습니다. 사실 이는 아주 간단한 아이디어를 도입하면 됩니다. 샘플링된 함수의 푸리에 변환으로부터 저희가 얻을 수 있는 결과는 기존 함수의 푸리에 변환 $F(\mu)$의 무한 반복이라고 하였습니다. 따라서, 만약 저희가 정확하게 한 개의 주기인 온전한 $F(\mu)$를 추출할 수 있다면 역푸리에 변환을 하여 샘플링되기 전 함수를 복원할 수 있습니다.
그런데 위의 그림에서 한 개의 주기를 온전히 추출할 수 있는 것은 오직 오버-샘플링과 임계 샘플링 뿐입니다. 언더-샘플링에서는 $F(\mu)$끼리 서로 영향을 주기 때문에 추출할 수 없죠. 이와 같이 샘플링되기 전에 함수로 완벽한 복원을 위한 조건을 설명하는 정리가 샘플링 정리(sampling theorem)입니다. 이를 좀 더 자세히 알아보도록 하겠습니다.
1. 샘플링 정리(sampling theorem)
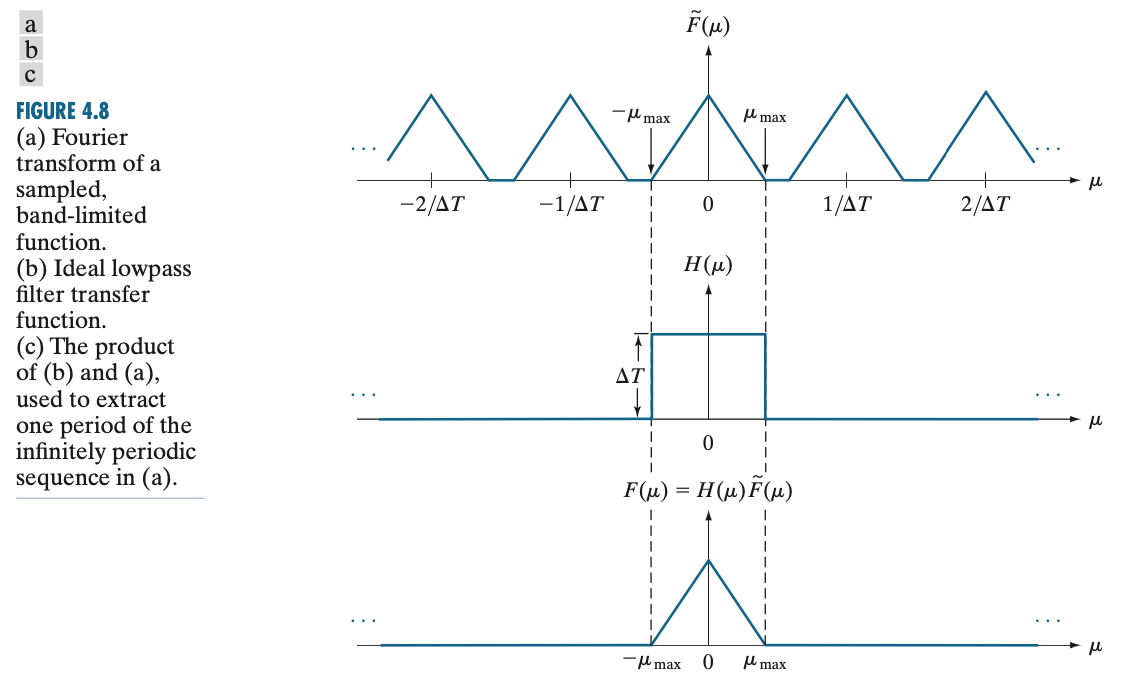
문제를 쉽게 하기 위해서 저희가 다루는 함수가 대역 제한 함수(band-limited function)이라고 가정하겠습니다. 대역 제한 함수란 어떤 함수 $f(t)$에 푸리에 변환을 적용했을 때, 유한 구간 $[-\mu_{\text{max}}, \mu_{\text{max}}]$를 제외한 나머지 구간에서는 0인 함수를 의미합니다. 이를 그림으로 표현하면 아래와 같습니다.

(a)는 위에서 언급한 조건에 부합하는 대역 제한 함수 $f(t)$에 푸리에 변환을 적용한 결과입니다. 특정 구간을 제외하고 나머지 구간에서는 0인 것을 볼 수 있습니다. (b)는 $f(t)$를 $\Delta T$의 샘플링 속도를 가지고 샘플링한 뒤 푸리에 변환을 적용한 결과입니다. 보시면 기존 함수 $f(t)$의 푸리에 변환 함수 $F(\mu)$가 무한 반복되고 있는 것을 볼 수 있죠. 그리고 동일한 함수가 주기 $\frac{1}{\Delta T}$를 가지고 반복되고 있습니다. 이때, $\mu \ge 0$에서 $F(\mu) = 0$이 되는 지점인 $\mu_{\text{max}}$는 $\Delta T$와 어떤 관계를 가지고 있을 까요? 이를 특정 주기를 가지고 무한히 반복되는 주기 함수의 성질을 이용하면 $\mu_{\text{max}} = \frac{1}{2\Delta T}$임을 알 수 있습니다.
따라서 대역 제함 함수로 한정지어 생각해보았을 때, 저희가 해당 함수를 샘플링한 뒤 다시 완벽히 복원하고 싶다면 어차피 $\mu_{\text{max}}$는 정해져있기 때문에 샘플링 속도 $\Delta T$를 아래와 같이 선택한다면 가능합니다.
$$2\mu_{\text{max}} < \frac{1}{\Delta T}$$
아마 많은 분들이 여기서 의문을 가지실 겁니다. 정확히 $2\mu_{\text{max}} = \frac{1}{\Delta T}$가 돼도 $F(\mu)$를 온전히 추출할 수 있기 때문에 샘플링 이전 함수로 완전 복원할 수 있지 않은지에 대해서 말입니다. 참고로 해당 조건을 만족하는 샘플링 속도 $\Delta T = \frac{1}{2\mu_{\text{max}}}$를 Nyquist 속도(Nyquist rate)라고 정의합니다. 하지만, Nyquist 속도로 샘플링하게 되면 특정 경우에는 완전 복원이 불가능하기 때문에 최소한 Nyquist 속도를 초과해야만 완전 복원이 가능합니다. 이후에 샘플링을 잘못해서 발생하는 문제인 앨리어싱(Aliasing)에 대해서 설명할 때 예시를 보여드리도록 하겠습니다.
이제 $F(\mu)$를 추출하는 과정을 수학적으로 모델링해보도록 하겠습니다. 대역 제한된 함수 $f(t)$에 푸리에 변환을 취하면 어차피 $[-\mu_{\text{max}}, \mu_{\text{max}}]$에서만 0이 아니기 때문에 저희가 필터링 함수 $H(\mu)$를 아래와 같이 정의하면 될 거 같습니다.
$$H(\mu) = \begin{cases} \Delta T &-\mu_{\text{max}} \le \mu \le \mu_{\text{max}} \\ 0 &\text{Otherwise} \end{cases}$$
여기서 1이 아닌 $\Delta T$가 붙은 이유는 샘플링된 함수의 푸리에 변환 $\tilde{F}(\mu)$에 $\frac{1}{\Delta T}$가 붙어있기 때문입니다. 따라서 Nyquist 속도 이상으로 입력 함수를 샘플링했다고 가정했을 때, $H(\mu)$를 이용해서 샘플링하면 아래와 같이 정리할 수 있습니다.
$$F(\mu) = H(\mu)\tilde{F}(\mu)$$
이제 여기에 역 푸리에 변환을 취해주면 저희가 얻고 싶어 했던 가장 처음에 얻었던 입력 함수를 얻을 수 있습니다.
$$f(t) = \int_{-\infty}^{\infty} F(\mu)e^{j2\pi\mu t} \; d\mu$$
이 전체 과정을 그림으로 정리하면 쉽게 이해하실 수 있습니다.
2. 앨리어싱(Aliasing)
눈치 채신분들은 미리 눈치채셨겠지만 샘플링 정리에서 대역 제한 함수로 가정하는 것은 매우 강력한 가정입니다. 왜냐하면 일반적으로 대부분의 함수는 대역 제한 함수가 아니기 때문이죠. 이는 곧 임의의 $f(t)$로 확장되어야 함을 의미하고 결과적으로 저희는 샘플링된 함수의 완전 복원은 "불가능"하게 됩니다. 아주 특수한 경우에서만 완전 복원이 가능한 것이죠. 그러므로 특수한 상황을 제외하고는 항상 어떤 인위적 구조물(artificial struct)이 발생하게 됩니다.
대역 제한 함수에서는 적어도 오버-샘플링 상황에서 완벽한 복원이 가능합니다. 하지만 언더-샘플링에서는 복원 자체가 불가능하게 됩니다. 이때 발생하는 문제를 앨리어싱이라고 합니다. 디지털 영상 처리에서는 앨리어싱뿐만 아니라 다양한 인위적 구조물이 존재합니다. 그중에서도 앨리어싱이 가장 대표적이죠. 앨리어싱이 발생하는 이유는 아래의 그림으로 인해 그렇습니다.
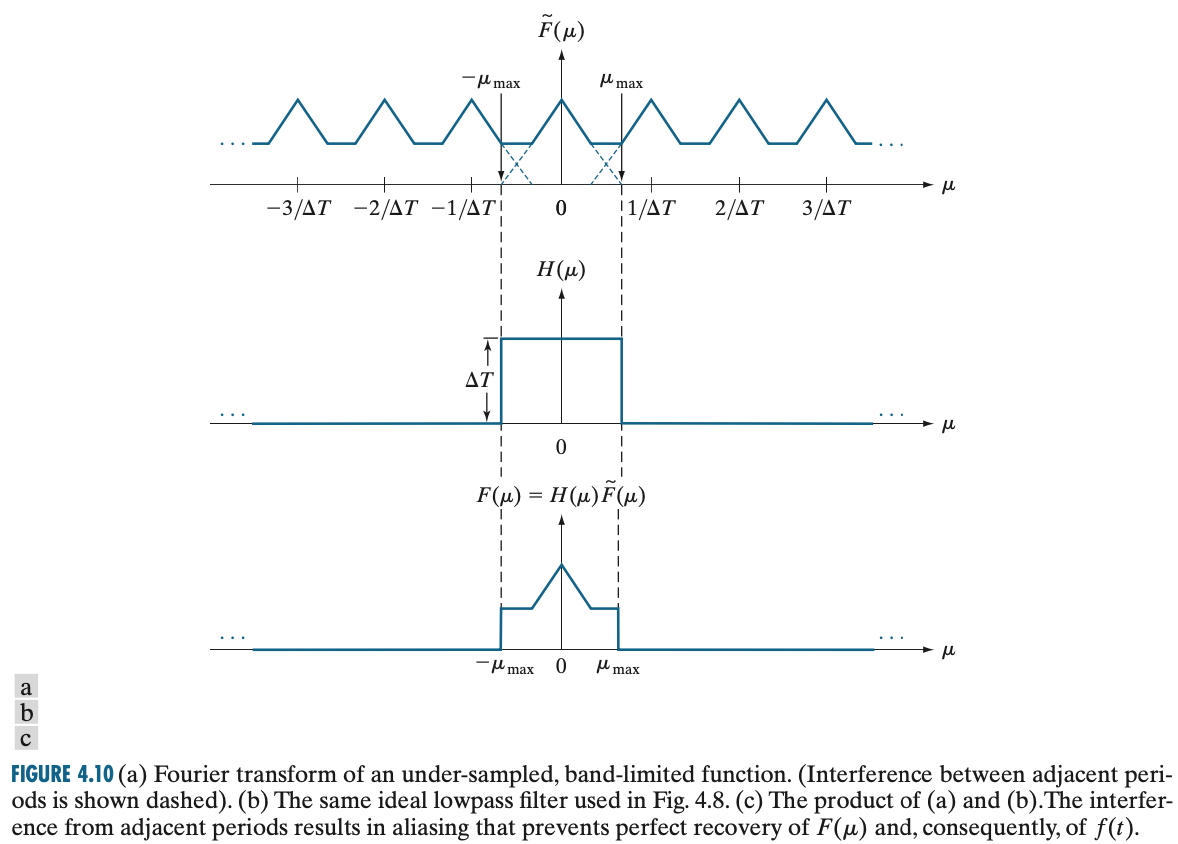
하지만, 처음에도 말씀드렸다시피 대역 제한된 함수가 아닌 일반적인 함수의 경우에는 애초에 완벽한 복원 자체가 불가능하기 때문에 앨리어싱이 항상 발생합니다. 따라서 이를 해결하기 위해서 샘플링 전에 안티-앨리어싱(anti-aliasing)을 통해 앨리어싱 효과를 감쇠시킬 수도 있습니다.
다음으로 Nyquist 속도에 맞춰서 샘플링 시 발생하는 문제를 설명해보도록 하겠습니다. 분명히 임계 샘플링을 그림으로 보았을 때는 딱히 문제가 발생할 것이라고는 예상하기 힘듭니다. 하지만 이는 간단하게 함수 하나를 주면 쉽게 이해 가능합니다.

일단, $f(t) = \sin{\left(\pi t\right)}$로 주어져있다고 가정하겠습니다. 해당 함수의 주기 $P = \frac{2\pi}{\pi} = 2$초입니다. 그리고 주파수는 $f = \frac{1}{P} = \frac{1}{2}$사이클/초입니다. 여기에서 샘플링된 함수를 완전복원하기 위해서는 샘플링 정리에 의해 해당 함수가 가지고 있는 최대 주파수 $f_{\text{max}}$의 2배로 설정하면 됩니다. 따라서 $\frac{1}{\Delta T} = 2 \times f_{\text{max}} = 2 \times \frac{1}{2} = 1 \Rightarrow \Delta T = 1$초보다 작은 값으로 설명하면 됩니다($\frac {1}{\Delta T} > 1 \leftrightarrow \Delta T < 1$). 그런데 여기에서 정확하게 $\Delta T = 1$이라고 가정해보도록 하겠습니다. 따라서 입력 함수로부터 샘플링되는 값은 중앙을 기준으로 했을 때 $\dots, \sin{\left(-\pi \right)}, \sin{\left(0\right)}, \sin{\left(\pi\right)}, \dots$이 됩니다. 그런데 그 값들은 전부 0입니다. 즉, 복원이 불가능하다는 의미죠.
3. 샘플링된 데이터로부터 함수의 복원
함수 복원을 조금 더 자세하게 설명해보도록 하겠습니다. 저희가 샘플링된 함수를 원래 함수로 복원하기 위해서 샘플링된 함수에 푸리에 변환을 적용해서 오버-샘플링, 즉 Nyquist 속도보다 큰 값으로 설정하면 완벽한 복원이 가능함을 설명하였습니다. 그리고 이를 컨볼루션 정리와 연계하여 수식으로 적으면 아래와 같습니다.
$$f(t) = \mathcal{F}^{-1}\{F(\mu)\} = \mathcal{F}^{-1}\{H(\mu)\tilde{F}(\mu)\} = h(t) * \tilde{f}(t)$$
이때, $\tilde{f}(t) = \sum_{n = -\infty}^{\infty} f(t)\delta(t - n\Delta T)$임을 기억하실 겁니다. 그러면 위의 식에서 $f(t) = h(t) * \sum_{n = -\infty}^{\infty} f(t)\delta(t - n\Delta T)$가 됩니다. 단순히 $\tilde{f}(t)$를 바꾼 것밖에 없습니다. 그리고 컨볼루션의 정의를 이용하면 아래와 같이 정리할 수 있습니다.
$$f(t) = h(t) * \sum_{n = -\infty}^{\infty} f(t)\delta(t - n\Delta T) = \int_{-\infty}^{\infty} h(\tau)\sum_{n = -\infty}^{\infty} f(t - \tau)\delta(t - n\Delta T - \tau) \; d\tau$$
$$ = \int_{-\infty}^{\infty} \sum_{n = -\infty}^{\infty}h(\tau) f(t - \tau)\delta(t - n\Delta T -\tau) \; d\tau$$
$$ = \sum_{n = -\infty}^{\infty} \int_{-\infty}^{\infty} \delta(t - n\Delta T - \tau)\left[h(\tau)f(t - \tau)\right] \; d\tau$$
$$ = \sum_{n = -\infty}^{\infty} \int_{-\infty}^{\infty} \delta(t - n\Delta T - \tau)\left[\text{sinc}\left(\frac{\tau}{\Delta T}\right)\right] \; d\tau$$
$$ = \sum_{n = -\infty}^{\infty} \text{sinc}\left[\frac{\left(t - n\Delta T\right)}{\Delta T}\right]f(n\Delta T)$$
위의 과정을 이해하시면 사실 상 임펄스 함수의 선별 특성, 컨볼루션 정의와 정리, 박스 필터의 푸리에 변환 결과인 $\text{sinc}$ 함수에 대해서 전부 이해하셨다고 보실 수 있습니다. 혹시 박스 필터의 푸리에 변환 유도 과정이 궁금하신 분은 링크를 참조해주시길 바랍니다.
위의 결과는 아래와 같이 정리할 수 있습니다.
$$f(t) = \sum_{n = -\infty}^{\infty} \text{sinc}\left[\frac{\left(t - n\Delta T\right)}{\Delta T}\right]f(n\Delta T)$$
이를 4가지로 해석해볼 수 있습니다.
- 복원된 함수 $f(t)$는 샘플 값들이 가중치로 곱해진 무한 합이다.
- 복원된 함수는 $\Delta T$의 정수배 위치에서 샘플 값과 동일하다.
- $k$가 정수일 때 모든 $t = k\Delta T$에 대해 $f(t) = f(k\Delta T)$이다.
- 복원된 함수 $f(t)$가 무한급수 이기 때문에 보간이 필요하다.
일단 1번에 대한 해석은 저희가 어떤 정수가 아닌 $t$에 값에 대한 복원된 함수의 값을 얻고 싶다고 가정하겠습니다. 그러면 $t$ 지점을 제외한 나머지 지점에서 $\text{sinc}$함수가 0이 아닙니다. 따라서 하나의 값을 복원하기 위해서 샘플링된 함수의 값을 $-\infty$부터 $\infty$까지 참조하게 되는 데 이때, 샘플 값이 가중치로 들어간다는 것이죠. 2번과 3번은 정수인 경우 $\text {sinc}(0) = 1$이기 때문에 명확합니다. 마지막으로 4번이 의미하는 바는 실질적으로 저희가 무한 개의 값이 아닌 유한 개의 값을 가지고 복원하기 때문에 이에 맞는 보간방법이 필요하다는 것입니다.
'image processing' 카테고리의 다른 글
| 디지털 영상 처리 - 이산 푸리에 변환과 이산 역푸리에 변환 구현 (0) | 2021.04.07 |
|---|---|
| 디지털 영상 처리 - 단일 변수 함수의 이산 푸리에 변환(Discrete Fourier Transform) (0) | 2021.04.05 |
| 디지털 영상 처리 - 샘플링과 샘플링된 함수의 푸리에 변환 (6) | 2021.03.31 |
| 디지털 영상 처리 - 주파수 공간 필터링 기초 2 (3) | 2021.03.29 |
| 디지털 영상 처리 - 주파수 공간 필터링 기초 1 (3) | 2021.03.27 |
