안녕하세요. 지난 포스팅의 디지털 영상 처리 - 샤프닝 공간 필터(Sharpening Spatial Filter) : 라플라시안 필터에서는 샤프닝의 기본 원리와 등방성 샤프닝 필터인 라플라시안 필터에 대해서 알아보았습니다. 오늘은 다른 샤프닝 기법은 언샤프 마스킹(Unsharp Masking)과 하이부스트 필터링(Highboost Filtering), 그리고 비등방성 필터(Anisotrophic filter)를 이용한 방법에 대해서 알아보도록 하겠습니다.
1. 언샤프 마스킹과 하이부스트 필터링(Unsharp Masking and Highboost Filtering)
지난 포스팅에서도 설명드렸다싶이 영상 샤프닝(Image Sharpening)이란 영상의 엣지를 찾아서 그 영역을 좀 더 강조하는 방법이라고 하였습니다. 언샤프 마스킹은 3가지 스텝으로 이루어집니다.
- 입력 영상 블러링 수행(= 언샤프닝)
- 블러링된 영상과 입력 영상 사이의 차이를 얻음(= 마스크)
- STEP 2에서 얻은 마스크를 입력 영상에 더하기
해당 알고리즘과 기존의 라플라시안 필터링의 차이점은 미분을 이용하지 않는다는 점입니다. 미분을 이용하는 방법은 명시적으로 엣지를 찾는 것과 동일하지만 미분을 사용하지 않고도 쉽게 엣지를 찾을수있습니다. 아래의 예제를 통해 설명드리겠습니다.
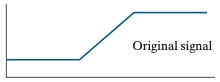
위의 그림과 같은 데이터가 입력되었다고 가정하겠습니다. 이제 해당 데이터에 블러링을 적용하면 됩니다. 블러링은 지난 포스팅의 평균 필터나 가우시안 필터를 사용하면 됩니다.

필터를 통해 블러링을 수행했기 때문에 입력 데이터에서 값이 변하는 지점은 약간 뭉툭해질것입니다. 이를 영상으로 생각해보시면 쉽게 이해할 수 있습니다. 영상에 블러링을 취하게 되면 영상 내의 엣지가 약간 흐려지는 현상을 보셨을 겁니다. 바로 그 현상을 1차원적으로 표현하면 위와 같이 그릴 수 있습니다.
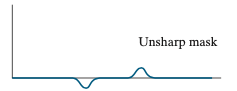
다음은 입력 데이터와 블러링된 데이터의 차이를 구합니다. 이를 언샤프 마스크라고 부릅니다. 이때, 값이 변하지 않는 지점에서는 블러링을 취하더라도 값이 똑같기 때문에 두 데이터를 뺄 때 0이 아닌 값을 가지는 지점은 오직 값이 변하는 지점 근처가 됩니다. 이 과정에서 저희는 엣지를 추출했다고 볼 수 있습니다.

이제 언샤프 마스크를 기존의 입력 영상에 더하면 저희가 원하는 값이 변하는 지점이 강조된 영상을 얻을 수 있는 것입니다. 이를 수식으로 표현해보겠습니다. 입력 영상을 $f(x, y)$, 블러링된 영상은 $\bar{f}(x, y)$라고 하겠습니다. 이제 두 영상을 빼면 저희는 언샤프 마스크 $g_{\text{mask}}(x, y) = f(x, y) - \bar{f}(x, y)$를 얻을 수 있습니다. 이제 $k \ge 0$에 대해서 언샤프 마스크를 입력 영상 $f(x, y)$에 더해주면 저희가 원하는 샤프닝된 영상을 얻을 수 있습니다.
$$g(x, y) = f(x, y) + k*g_{\text{mask}}(x, y)$$
이때, $k$의 값에 따라서 언샤프 마스킹, 그리고 하이부스트 필터링으로 나뉩니다. 만약 $k = 1$이라면 지금까지 저희가 해온 언샤프 마스킹이 되는 것이고 $k > 1$이라면 하이부스트 필터링이 됩니다. 하이부스트(Highboost)란 어떤 것을 더 크게 강조한다라고 볼 수 있습니다. $k$의 값이 커지면 커질수록 언샤프 마스크의 엣지 근처의 값이 더 강조하기 때문에 저희가 원하는 만큼 엣지가 더 강조된 샤프닝 영상을 얻을 수 있습니다.

위에서 왼쪽의 영상이 입력이면 블러링 적용하여 가운데 영상을 얻고 입력 영상과 블러링된 영상 사이의 차이를 구하면 오른쪽 영상을 얻을 수 있습니다. 이 영상이 언샤프 마스크가 되는 것이죠.

이제 언샤프 마스크를 입력 영상에 더해주면 됩니다. 이때, 그냥 더해주면 언샤프 마스킹이 되고, $k \ge 1$인 값을 곱하여 더해주면 하이부스트 필터링이 됩니다. 왼쪽 영상은 언샤프 마스킹을 수행한 영상이고 오른쪽 영상은 하이부스트 필터링을 위해서 $k = 4.5$를 곱하여 얻은 영상입니다. 확실이 하이부스트 필터링이 언샤프 마스킹에 비해서 엣지 영역이 더 많이 강조되어 뚜렷해보이는 거 같습니다.
2. 비등방성 필터(Anisotrophic filter) - 로버츠 연산자와 소벨 연산자
지난 포스팅에서는 등방성 필터의 대표주자인 라플라시안 필터를 이용한 영상 샤프닝을 소개하였습니다. 오늘은 비등방성 필터에 대해서 알아보도록 하겠습니다. 비등방성 필터라고 해서 등방성 필터와 크게 다르지 않습니다. 등방성 필터는 2차 미분인 라플라시안(Laplacian)을 활용하지만 비등방성 필터는 1차 미분인 그래디언트(Gradient)를 이용한다는 점이 다릅니다. 그래디언트는 머신러닝을 공부해보셨다고 무조건 들어보는 개념으로써, 기하학적인 의미로는 어떤 함수의 $(x, y)$지점에서 가장 빠르게 값이 증가하는 방향을 나타냅니다. 그래디언트는 아래와 같이 벡터로 정의됩니다.
$$\nabla f = \text{grad}(f) = \left[f_{x} f_{y}\right]^{T} = \left[\frac{\partial f}{\partial x} \frac{\partial f}{\partial y}\right]^{T}$$
여기서 $\frac{\partial f}{\partial x}$를 보도록 하겠습니다. 해당 미분은 $y$ 방향을 전혀 고려하지 않고 오직 $x$ 방향에서의 미분을 수행하기 때문에 $x$ 방향에서의 변화율을 측정합니다. 이를 영상으로 대입해보면 오직 가로 방향의 엣지만 감지한다는 것을 의미합니다. 하지만 저희는 세로 방향의 엣지도 감지하고 싶습니다. 이를 위해서 $x$와 $y$ 방향 모두의 미분을 활용하기 위해서 그래디언트의 크기(Magnitude)를 활용합니다. 이러한 특징은 비등방성 필터를 사용하는 경우 항상 적용됩니다. 그래디언트의 크기는 크게 2가지로 나타낼 수 있습니다.
$$M(x, y) = \text{mag}(\nabla f) = \sqrt{f_{x}^{2} + f_{y}^{2}}$$
$$M(x, y) \approx |f_{x}| + |f_{y}|$$
하지만 일반적으로 위의 수식을 더 많이 사용하는 편입니다. 이와 같이 그냥 그래디언트를 그대로 사용하는 방법도 있지만 이러한 개념을 바탕으로 파생된 유명한 필터가 2가지가 존재합니다. 바로 로버츠 교차-그래디언트 연산자(Roberts cross-gradient operator)와 소벨 연산자(Sobel operator)입니다. 이를 필터로 표현하면 아래와 같습니다. 로버츠 연산자는 $2 \times 2$, 소벨 연산자는 $3 \times 3$으로 영상의 각각 2개의 필터를 적용한 후 위의 수식을 사용하면 원하는 결과를 얻을 수 있습니다.

마지막으로 소벨 연산자를 이용한 엣지 감지 결과를 보시면 아래의 결과를 얻을 수 있습니다.

'image processing' 카테고리의 다른 글
| 디지털 영상 처리 - 공간 개선 방법 결합 (0) | 2021.03.24 |
|---|---|
| 디지털 영상 처리 - 샤프닝 공간 필터 구현 (0) | 2021.03.22 |
| 디지털 영상 처리 - 샤프닝 공간 필터(Sharpening Spatial Filter) : 라플라시안 필터 (2) | 2021.03.20 |
| 디지털 영상 처리 - 스무딩 공간 필터 구현 (0) | 2021.03.19 |
| 디지털 영상 처리 - 스무딩 공간 필터(Smoothing Spatial Filter) (0) | 2021.03.17 |
