안녕하세요. 지난 포스팅의 디지털 영상 처리 - 스무딩 공간 필터 구현에서 선형/비선형 스무딩 필터를 간단하게 구현해보고 테스트까지 해보았습니다. 스무딩 필터링은 결국 영상 블러링을 의미한다고 하였습니다. 그렇다면 이와는 반대로 영상이 좀 더 뚜렷하게 보이게 만드는 방법은 없을까요? 오늘 소개할 샤프닝 공간 필터를 이용하면 충분히 가능합니다.
샤프닝 공간 필터의 기본 원리는 영상 내의 픽셀 강도의 변화를 강조하는 것입니다. 그렇다면 영상 내에 픽셀 강도의 변화가 가장 큰 곳은 어디일까요? 바로 엣지입니다. 샤프닝 공간 필터를 엣지를 강조하여 사람이 보았을 때 좀 더 뚜렷하게 보이는 것처럼 만들어주는 방법입니다. 따라서 저희는 이제부터 엣지(edge)를 얻어내는 방법이 필요합니다. 이를 위해서는 미분이 필요하기 때문에 디지털 영상에서 미분이 정의될 수 있도록 몇 가지 가정부터 하도록 하겠습니다.
먼저, 디지털 영상에서 1차 미분(first derivative)은 아래의 3가지 조건을 만족해야합니다.
- 픽셀 강도가 일정한 영역에서의 1차 미분은 0이다.
- 픽셀 강도가 변화하는 지점(step, ramp)에서의 1차 미분은 0이 아니다.
- 모든 ramp 구간에서의 1차 미분은 항상 0이 아니다.
여기서 나온 ramp와 step은 디지털 영상에서 2차 미분(second derivative)의 조건을 명시한 후 설명하도록 하겠습니다. 아직은 간단하게 영상 내에 픽셀 강도가 변하는 구간이라고 생각하시면 됩니다. 2차 미분 역시 1차 미분과 마찬가지로 아래의 3가지 조건을 만족해야 합니다.
- 픽셀 강도가 일정한 영역에서의 2차 미분은 0이다.
- step이나 ramp의 시작과 끝 지점에서의 2차 미분은 0이 아니다.
- ramp 구간이 constant slope를 가지고 픽셀 강도가 변화한다면 그 구간의 2차 미분은 0이다.
위와 같은 조건을 두고 1차 미분과 2차 미분을 어떤 이산값을 가지는 1차원 함수 $f$에 대해서 정의하면 아래와 같습니다. 이러한 수식을 유도하는 수치적 기법이 있으나 이 부분은 과감하게 생략하고 이와 같이 정의하면 1차 미분, 2차 미분의 조건이 전부 성립한다는 것으로 받아들이시면 됩니다.
- $\frac{\partial f}{\partial x} = f(x + 1) - f(x)$
- $\frac{\partial^{2} f}{\partial x^{2}} = f(x + 1) + f(x - 1) - 2f(x)$
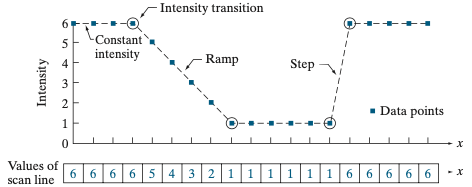
일단, 실제 쉬운 예제를 통해서 미분을 진행해보도록 하겠습니다. 상단의 그림을 참고해주세요. 미분 조건을 말씀드렸을 때 ramp와 step에 대해서 말씀드렸습니다. step은 영상 내에서 $x$ 축에서 한 칸만 움직여도 굉장히 큰 변화가 생기는 지점을 의미합니다. 그리고 ramp는 step과는 다르게 비교적 완만한 변화를 가지는 구간을 의미합니다.
위와 같은 데이터가 주어져있을 때 1차 미분을 진행해보도록 하겠습니다. 일단 $x = 0$부터 해볼까요? 저희가 정의한 수식을 사용하면 $\frac{\partial f}{\partial x} |_{x=0} = f(1) - f(0) = 6 - 6 = 0$입니다. 즉, $x = 0$에서는 데이터에 어떠한 변화도 없음을 알 수 있습니다. 물론 이렇게 일일이 계산할 수도 있지만 저희는 1차 미분의 첫 번째 조건을 활용하면 $x = 0, 1, 2$에서의 값은 일정하기 때문에 1차 미분의 결과가 0이 나올 것입니다(실제로 계산해봐도 0이 나옵니다!). 또한 일정한 구간인 $x = 8, 9, 19, 11, 12$, 그리고 $x = 14, 15, 16, 17$에서도 1차 미분은 0입니다. 아주 간단하죠? 다음으로는 변화가 시작되는 지점을 보도록 하겠습니다. $x = 3$에서의 1차 미분은 $\frac{\partial f}{\partial x} |_{x=3} = f(4) - f(3) = 5 - 6 = -1$로 -1만큼 변화하였음을 볼 수 있습니다. 또한 $x = 4, 5, 6, 7$에서도 마찬가지로 -1만큼의 변화를 하고 있죠. 다음으로는 step 지점 $x = 13$에서의 1차 미분은 $\frac{\partial f}{\partial x} |_{x=13} = f(14) - f(13) = 6 - 1 = 5$로 +5만큼의 큰 변화가 있음을 볼 수 있습니다. 2차 미분도 동일하게 하면 저희는 아래와 같은 표를 얻을 수 있습니다.

2차 미분은 1차 미분과는 다르게 앞-뒤 데이만 보는 것이 아니라 현재 데이터와 이전 데이터, 이후 데이터의 정보를 함께 사용하기 때문에 결과가 달라집니다. 일정한 값의 구간에서는 동일하게 0이지만, 2차 미분에서는 ramp 구간의 시작 지점, 끝 지점만 미분이 0이 아니고 내부 구간은 일정하게 변화하게 때문에 0이 됩니다. 또한 step 지점에서도 step이 시작되는 $x = 13$, 그리고 step이 끝나는 $x = 14$에서만 미분 값이 0이 아님을 볼 수 있습니다.
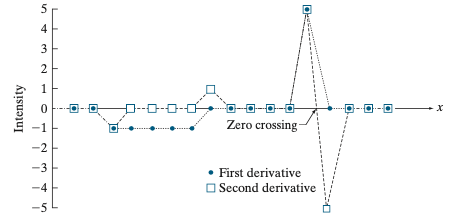
1차 미분과 2차 미분의 결과를 그래프로 그려보면 상단의 그림과 같습니다. 2차 미분의 경우에는 급격하게 값이 변화하는 step 지점에서 미분값이 +5에서 -5로 변화하면서 0을 지나게 됩니다. 이 현상을 "zero crossing"이라고 부르게 됩니다. 이게 왜 중요한 지는 다시 한번 저희의 목표를 생각해보시면 됩니다. 저희는 영상 샤프닝을 위해서 엣지를 찾고자 하였습니다. 그런데 엣지의 가장 중요한 특성은 굉장히 가파른 픽셀 강도 변화를 보이고 있죠. 따라서 디지털 영상 전체에 2차 미분을 적용한 뒤 zero crossing이 발생하는 지점을 찾으면 엣지를 찾을 수 있을 것입니다. 실제로 이러한 방법을 사용해서 영상 샤프닝을 수행하니 꼭 기억해주시길 바랍니다.
영상 내에서 엣지를 찾는 필터는 크게 2가지가 존재합니다. 각각 등방성(isotrophic), 비등방성(anisotrophic) 필터입니다. 등방성 필터는 회전 불변성(rotation invariant)를 가지는 필터로써 중앙을 중심으로 어떤 각도로 회전시켜도 동일한 필터가 유지되는 특성을 가지고 있습니다. 비등방성 필터는 회전 불변성을 가지고 있지 않아 회전 시 동일한 필터가 아닙니다. 이때, 가장 대표적인 등방성 필터가 바로 라플라시안(Laplacian) 필터입니다.
대학교 공대나 자연대를 나오신 분들은 라플라시안에 대해서 익히 들어보셨을 겁니다. 바로 2차 미분을 다르게 말한 것입니다. 그런데 2차 미분의 개념을 처음 알려드렸을 때는 1차원에서 정의가 되었지만 저희는 이제 2차원 데이터인 디지털 영상을 다루기 위해서 라플라시안을 사용하게 됩니다. 이를 수식으로 표현하면 아래와 같습니다.
$$\Delta f = \nabla^{2}f = \frac{\partial^{2} f}{\partial x^{2}} + \frac{\partial^{2} f}{\partial y^{2}}$$
하지만 저희는 이산 데이틀 다루기 때문에 이에 맞게 변형시켜야 합니다. 먼저, $\frac{\partial^{2} f}{\partial x^{2}}$과 $\frac{\partial^{2} f}{\partial y^{2}}$부터 바꾸면 아래와 같습니다.
$$\frac{\partial^{2} f}{\partial x^{2}} = f(x+1, y) + f(x-1, y) - 2f(x, y)$$
$$\frac{\partial^{2} f}{\partial y^{2}} = f(x, y+1) + f(x, y-1) - 2f(x, y)$$
그 다음으로 두 결과를 하나로 합치면 됩니다.
$$\Delta f = f(x+1, y) + f(x-1, y) + f(x, y+1) + f(x, y-1) - 4f(x, y)$$
수식을 자세히보면 $(x, y)$를 지점으로 4-이웃 픽셀들을 고려하여 계산하게 됩니다. 그래서 이를 하나의 커널로 표현하면 저희는 아래의 결과를 얻을 수 있습니다.

가장 기본적인 라플라시안 필터는 (a)이지만 8-이웃을 고려하여 (b)와 같이 쓰는 경우도 있으며 중앙 가중치와 이웃 가중치의 부호를 바꾸어서 (c), (d)와 같이 사용하는 경우도 있습니다. 어떤 것을 쓸지는 엣지가 잘 추출되는 것으로 사용하면 되겠죠? 이제 라플라시안 필터를 사용하여 엣지를 얻었다고 가정하면 그 엣지를 그냥 입력 영상에 그대로 더하면 끝입니다. 하지만 상단의 커널 중 (a), (b)를 쓰면 그냥 더하면 되지만 (c), (d)를 쓰는 경우에는 빼주어야 합니다. 샤프닝된 영상을 $g(x, y)$라고 했을 때, 이를 표현하면 아래와 같습니다.
$$g(x, y) = f(x, y) + c\left[\Delta f(x, y)\right]$$
이때, (a)나 (b) 커널을 쓰면 $c = 1$을 쓰면 (c)나 (d) 커널을 쓰면 $c = -1$을 사용하면 됩니다. 이제 실제 결과를 보도록 하겠습니다.

먼저, 왼쪽으로 입력 영상일 때, 여기에 라플라시안 커널 (a)을 적용하면 오른쪽의 엣지 영상을 얻을 수 있습니다. 이제 오른쪽 영상을 왼쪽 영상에 $c = 1$로 해서 더하면 되겠죠? 그러면 아래의 결과를 얻을 수 있습니다.

왼쪽 영상은 (a) 커널을 사용한 결과이고 오른쪽 영상은 (b) 커널을 사용하면 얻을 수 있습니다. 눈으로 보았을 때는 (b) 커널을 사용했을 때 조금 더 샤프닝된 결과를 얻을 수 있습니다. 참고로 (b) 커널을 사용한 엣지 영상은 아래와 같습니다.

'image processing' 카테고리의 다른 글
| 디지털 영상 처리 - 샤프닝 공간 필터 구현 (0) | 2021.03.22 |
|---|---|
| 디지털 영상 처리 - 샤프닝 공간 필터(Sharpening Spatial Filter) : 언샤프닝 마스킹, 하이부스팅 필터링, 비등방성 필터 (0) | 2021.03.21 |
| 디지털 영상 처리 - 스무딩 공간 필터 구현 (0) | 2021.03.19 |
| 디지털 영상 처리 - 스무딩 공간 필터(Smoothing Spatial Filter) (0) | 2021.03.17 |
| 디지털 영상 처리 - 공간 필터링 기초 (3) | 2021.03.15 |
