안녕하세요. 지난 포스팅의 디지털 영상 처리 - 히스토그램 처리 함수 구현을 마지막으로 히스토그램 처리와 관련된 이론과 실제 구현을 해보았습니다. 오늘부터는 히스토그램 처리가 아닌 공간 필터링 기법에 대해서 알아보도록 하겠습니다. 사실 지난 포스팅의 디지털 영상 처리 - 지역적 히스토그램 처리를 이해하셨다면 쉽게 이해할 수 있습니다. 왜냐하면 거의 비슷한 알고리즘을 사용하기 때문입니다. 다른 점은 내부 연산이 다르며 동일한 점은 영상보다 작은 크기의 윈도우를 정의하고 한 픽셀씩 이동시키면서 진행합니다. 바로 알아보도록 하죠.
1. 공간 필터링의 메커니즘(The Machanics of Spatial Filtering)

공간 필터링은 상단의 그림을 보시면 더욱 쉽게 이해하실 수 있습니다. 일단 2가지는 먼저 정의되어야합니다. (1). 특정 픽셀을 중심으로 한 이웃 픽셀들의 모음이 필요합니다. 그리고 (2). 해당 모음에 어떤 연산을 적용할 것인지입니다. 이 두 가지는 먼저 정의되어 필터링이 수행됩니다. 이를 통해서 새로운 영상에서 이웃의 중심 좌표와 동일한 좌표를 가지면 필터링 연산의 결과를 값으로 하는 새로운 화소가 생성됩니다. 이러한 과정이 윈도우가 입력 영상 전체를 훑고 지나가면서 하나의 새로운 영상이 만들어지는 것이죠.
이때, 영상 화소들에 적용되는 연산이 선형적(linear)라면 그 필터를 선형 공간 필터(linear spatial filter)라고 부릅니다. 만약 비선형적(nonlinear)라면 비선형 공간 필터(nonlinear spatial filter)라고 부릅니다.
상단의 그림을 보시면 임의의 픽셀 $(x, y)$에서 입력 영상의 값을 $f(x, y)$, 윈도우 내부의 값을 $w(i, j)$, 출력 영상의 값을 $g(x, y)$라고 했을 때 3개 사이에는 아래의 관계식이 성립하게 됩니다.
$$g(x, y) = w(-1, -1)f(x - 1, y - 1) + w(-1, 0)f(x - 1, y) + \cdots + w(0, 0)f(x, y) + \cdots + w(1, 1)f(x + 1, y + 1)$$
여기서 관찰할 점은 $g(x, y)$가 $w(i, j)$, 그리고 $f(x + i, y + j)$ 사이의 곱(Product)을 적용하고 그 결과를 합(Sum)을 하는 것입니다. 그래서 일반적으로 이러한 구조의 연산을 곱의 합(Sum-Of-Product; SOP)라고 부릅니다. 즉, 모든 공간 필터링은 기본적으로 입력 영상의 작은 크기의 영역에서 미리 정의된 연산과 윈도우를 통해 SOP를 적용하여 하나의 화소를 새로 생성하는 것이라고 정리할 수 있습니다. 이때, 어떤 연산을 적용하느냐에 따라서 선형 필터링과 비선형 필터링으로 나뉘게 되는 것이죠. 아주 간단하지 않나요? 하지만, 상단의 수식을 조금 더 정리를 시켜야 합니다.
일반적으로 윈도우의 중앙 계수 $w(0, 0)$는 $(x, y)$ 위치의 화소와 정렬됩니다. 이에 고안하여 크기가 $m \times n$인 윈도우에 대해서 $m = 2a + 1, n = 2b + 1$로 가정하도록 하겠습니다. 이때, $a, b$는 각각 1 이상의 정수입니다. 즉, 최소 윈도우의 크기는 $3 \times 3$이고 가로, 세로 크기는 항상 홀수여야 한다는 것입니다. 굳이 홀수로 정하는 것은 명확한 이유가 있습니다. 다시 한번 윈도우의 중앙 계수인 $w(0, 0)$와 $(x, y)$ 위치의 화소가 정렬되어야 한다는 점을 상기해주시길 바랍니다. 만약, 윈도우의 크기가 짝수를 가지게 되면 정렬되지 않을 것입니다. 이러한 이유로 홀수 크기의 윈도우를 사용하는 것이죠. 실제로 딥 러닝의 합성곱 신경망의 커널 사이즈를 정의할 때는 홀수 크기를 사용하는 것도 동일한 이유가 됩니다. 이와 같은 가정을 통해서 저희는 SOP 수식을 아래와 같이 간단하게 바꾸어볼 수 있습니다.
$$g(x, y) = \sum_{s = -a}^{a}\sum_{t = -b}^{b} w(s, t)f(x + s, y + t)$$
2. 공간 코릴레이션과 컨볼루션(Spatial Correlation and Convolution)
사실 지금까지 저희가 적용한 SOP 수식은 공간 코릴레이션입니다. 컨볼루션은 코릴레이션을 적용하기 전에 윈도우가 180 회전한다는 점 빼고는 완전히 동일한 메커니즘으로 진행합니다. 바로 2차원 영상에 적용하면 많이 헷갈리기 때문에 비교적 간단한 1차원 벡터를 통해 두 개의 차이점에 대해서 알아보도록 하겠습니다.

먼저, 상단의 그림과 같이 4번째 위치에서만 1이고 나머지 위치에서는 0인 어떤 벡터를 보도록 하겠습니다. 그리고 윈도우는 $1, 2, 4, 2, 8$로 5개의 값을 가지는 간단한 윈도우를 고려해보도록 하겠습니다. 그러면 왼쪽과 같이 $w$에 아무것도 적용하지 않고 그냥 저희가 아는 방식으로 통과시키면 이를 공간 코릴레이션이 되는 것이고 오른쪽과 같이 필터링을 적용하기 전에 $w$를 180도로 회전한 뒤 SOP를 적용하면 이를 공간 컨볼루션이라고 부르게 됩니다.

이제 통과시키려고 하는 데 위쪽의 그림을 보시면 코릴레이션과 컨볼루션 모두 2개의 윈도우 값이 밖으로 삐져나와있습니다. 이를 처리하기 위해서 아무런 의미가 없는 값인 0을 양쪽에 동일한 크기로 채워주는 패딩(padding)을 적용해줍니다. 즉, 윈도우의 크기에 따라서 이 패딩을 얼마나 적용해야 할지 달라지게 됩니다.

나머지는 저희가 아던대로 필터링을 적용합니다. 그러면 가장 아래의 코릴레이션과 컨볼루션의 결과를 얻을 수 있습니다.

그런데 저희가 입력 벡터의 양쪽으로 두 칸씩 0으로 채웠습니다. 그래서 상단의 그림처럼 SOP 결과에 패딩을 적용한 만큼 다시 패딩을 적용해주기도 합니다. 그러나 일반적으로 위와 같이 패딩을 추가로 하지는 않고 끝냅니다. 두 연산의 차이를 비교해보면 코릴레이션은 필터링을 적용시킨 윈도우의 가중치가 180도 뒤집힌 것을 볼 수 있습니다. 그리고 컨볼루션은 윈도우의 가중치의 위치가 바뀌지 않고 보존되어 있죠.
일련의 과정을 2차원 행렬로 확장시켜보도록 하겠습니다.
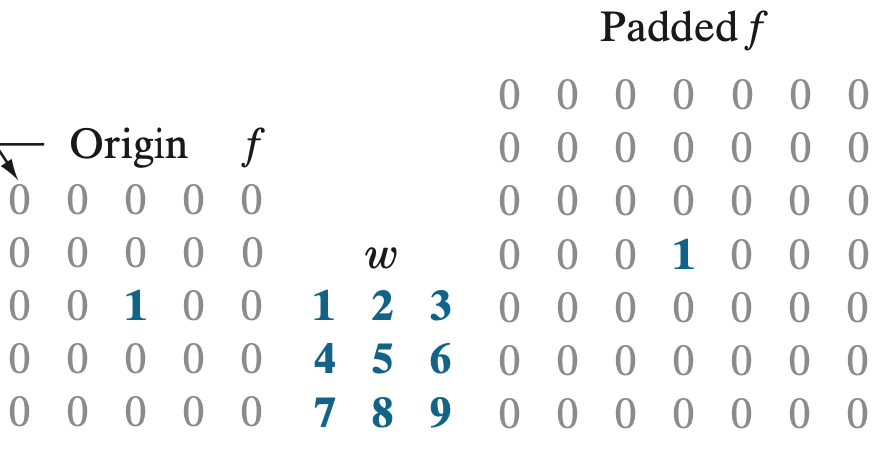
상단의 그림과 같이 행렬의 원점을 중심으로 필터링을 적용해야하지만 그러면 윈도우의 가중치 몇 개가 행렬 밖으로 나오게 됩니다. 이러한 문제를 막기 위해서 오른쪽 그림과 같이 윈도우의 가중치 전체를 커버할 수 있도록 0으로 패딩을 해주게 됩니다.

먼저, 코릴레이션부터 보도록 하겠습니다. 이전에 말씀드렸다시피 가중치를 그냥 행렬에 통과시키면 됩니다. 그 결과 윈도우 자체가 180도가 회전되었습니다.

이번에는 컨볼루션입니다. 윈도우를 통과시키기 전에 윈도우를 180도 회전시킨 후 통과시키는 것을 볼 수 있습니다. 그 결과 기존의 윈도우가 튀어나오게 됩니다.
코릴레이션은 두 영상 사이의 일치 정도를 수치화하는 데 사용될 수 있습니다. 만약 두 영상이 주어졌을 때, 코릴레이션이 최대가 되기 위해서는 두 영상이 일치해야 최대화가 될 것입니다. 또한 컨볼루션은 나중에 알아볼 주파수 필터링에서 매우 중요한 개념으로써 반드시 숙지해야 합니다. 지금까지 알아본 코릴레이션과 컨볼루션을 수식으로 나타내면 아래와 같습니다.
$$w(x, y) \circledast f(x, y) = \sum_{s=-a}^{a}\sum_{t=-b}^{b} w(s ,t)f(x+s, y+t)$$
$$w(x, y) * f(x, y) = \sum_{s=-a}^{a}\sum_{t=-b}^{b} w(s, t)f(x - s, y - t)$$
첫번째 수식이 코릴레이션이고 두 번째 수식이 컨볼루션입니다. 차이점은 컨볼루션을 적용하기 전에는 원래 윈도우를 180도 회전시킨 뒤 적용해주어야 하지만 관례 상 그냥 영상 자체를 180도로 회전시켜서 컨볼루션을 적용해주게 됩니다.
3. 선형 필터링의 벡터 표현(Vector Representing of Linear Filtering)
보통 저희가 넘파이나 매트랩을 이용해서 많이들 구현을 하게 되는데 단순 for 문을 이용한다면 1개의 영상에 필터링을 적용하려면 기본적으로 2개의 for 문이 필요합니다. 가로 세로에 대해서 각각 적용해주어야 하기 때문이죠. 이를 한방에 처리할 수 있도록 바꾸어준 것이 벡터로 표현한 것입니다. 일반적으로 SOP를 벡터화시켜서 표현하면 아래와 같습니다. 이와 같은 방법으로 표기방식도 좀 더 쉬워지겠죠.
$$R = w_{1}z_{1} + \cdots + w_{mn}z_{mn} = \sum_{k=1}^{mn} w_{k}z_{k} = \mathbf{w}^{T}\mathbf{z}$$
'image processing' 카테고리의 다른 글
| 디지털 영상 처리 - 스무딩 공간 필터 구현 (0) | 2021.03.19 |
|---|---|
| 디지털 영상 처리 - 스무딩 공간 필터(Smoothing Spatial Filter) (0) | 2021.03.17 |
| 디지털 영상 처리 - 히스토그램 처리 함수 구현 (0) | 2021.03.13 |
| 디지털 영상처리 - 지역적 히스토그램 처리 (0) | 2021.03.11 |
| 디지털 영상 처리 - 히스토그램 지정(Histogram Matching) (0) | 2021.03.10 |
