안녕하세요. 오늘은 지난 기초통계학[2].확률 기초(https://everyday-image-processing.tistory.com/7)에 이어서 조금 더 어려운 조건부 확률과 독립, 베이지안 법칙에 대해서 알아보겠습니다. 너무 어렵진 않으니 겁먹지 마세요!
1. 조건부 확률
조건부 확률을 간단하게 설명하면 어떤 추가적인 정보가 주어졌을 때, 사건이 일어날 확률입니다.
예를 들어 공평한 동전 3개를 던진다고 가정하겠습니다. 그럼 지난 시간에 확인했듯이 표본 공간, $\Omega = \{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT\}$가 됩니다. 이 중에서 3번 모두 앞면(H)가 나오는 경우의 수는 1가지이기 때문에 $\frac{1}{8}$이 됩니다.
그런데 여기서 조건, '첫 번째 던졌을 때는 무조건 앞면이 나온다.'이 추가되면, 새로운 표본 공간을 정의합니다. $\Omega^{'} = \{HHH, HHT, HTH, HTT\}$가 되며, 이 중에서 3번 모두 앞면이 나오는 경우의 수는 1가지이므로 $\frac{1}{4}$가 됩니다.
위와 같이 추가적인 조건하에 사건이 일어날 확률을 구하므로 '조건부 확률(conditinal probability)'라고 말합니다.
방금 전의 예시를 더 공식적인 표기로 사용하면 사건 A를 '모든 동전이 앞면이 나온다.', 그리고 사건 B를 '첫번째 동전이 앞면이 나온다.' 이를 집합으로 표현하면 $A=\{HHH\}$, $B=\{HHH, HHT, HTH, THH\}$가 됩니다.
여기서 사건 B가 발생할 때, 사건 A가 발생할 확률은 $P(A|B)$로 표기합니다.

왼쪽 그림에서 A가 발생한 확률은 A의 영역만큼입니다. 이때, $P(A|B)$는 B라는 제한사항이 있는 상태에서 A가 생길 확률인 것을 알 수 있습니다. 따라서 $P(A|B)$는 $\frac{P(A \cap B)}{P(B)}$와 같습니다.
오른쪽 그림은 방금 동전 예를 도식화한 결과입니다. 왼쪽 그림과는 다르게 사건 A가 사건 B의 부분집합이기 때문에 더 단순한 예라고 할 수 있습니다.
- 조건부 확률 : 사건 A와 사건 B가 주어졌을 경우, 사건 B가 조건일 때, 사건 A가 일어날 확률인 조건부 확률(conditional probability)는 $P(A|B) = \frac{P(A \cap B)}{P(B)}$가 되며 $P(B)$는 당연히 0이 되서는 안됩니다.
2. 조건부 확률에서의 곱셈 법칙
- 곱셈 법칙(Multiplicative rule) : $P(A \cap B) = P(A|B)P(B)$
위의 식은 사실 조건부 확률의 정의를 통해 얻을 수 있는 공식입니다. 단순하고 양변에 $P(B)$를 곱하면 나오는 공식이죠. 몇 가지 예제를 통해 적응을 해봅시다!
Ex1. 52장의 카드가 있는 덱에서 2장을 선택한다고 가정하겠습니다. 이때, $S_{1}$='첫번째 카드가 스페이드', $S_{2}$='두번째 카드가 스페이드'라고 가정하고, $P(S_{2}|S_{1})$를 구해봅시다.
Answer
저희는 2가지 접근법을 통해 해결할 수 있습니다. 직접 세기와 공식 사용하기.
1). 직접 세는 경우
$S_{1}$으로 인해 첫번째 카드는 항상 스페이드가 나오는 것을 알게되었으므로, 13장의 스페이드 카드 중 1장의 스페이드 카드가 없어졌습니다. 따라서 전체 52장의 카드는 51장으로, 13장의 스페이드 카드는 12장으로 변화하였습니다. 그러므로 두번째 카드가 스페이드일 확률은 $\frac{12}{51}$가 되는 것이죠.
2). 공식을 적용하는 경우
공식을 사용하기 위해 먼저, $P(S_{1})$, $P(S_{1} \cap S_{2})$를 계산해야합니다.
- $P(S_{1})$ = 첫번째로 52장의 카드 중 스페이드를 선택할 확률
- $P(S_{1} \cap S_{2})$ = 첫번째로 52장의 카드 중 스페이드를 뽑으면서 두번째로 51장의 카드 중 스페이드를 선택할 확률
따라서 $P(S_{1})=\frac{13}{52}$, $P(S_{1} \cap S_{2})=\frac{13}{52}\frac{12}{51}$입니다.
이제 조건부 확률 공식을 사용하면, $P(S_{2}|S_{1})=\frac{P(S_{1} \cap S_{2})}{P(S_{1})}=\frac{12}{51}$로 첫번째 결과가 같은 것을 볼 수 있습니다.
물론 이번 예제의 경우에는 직접 세는 것이 더 간단해보이지만 더 복잡한 문제의 경우 공식을 적용할 때 더 빨리 계산되는 경우가 많습니다.
3. 총 확률의 법칙
표본 공간($\Omega$)이 서로 disjoint한 3개의 사건 $B_{1}$, $B_{2}$, $B_{3}$으로 나누어져있다고 가정하겠습니다. 그렇다면, 표본 공간 내에서 임의의 사건 A가 일어날 확률은 아래와 같습니다.
$$P(A)=P(A \cap B_{1})+P(A \cap B_{2})+P(A \cap B_{3})$$
이를 다시 곱셈 법칙으로 풀어서 쓸 수 있습니다.
$$P(A)=P(A|B_{1})P(B_{1})+P(A|B_{2})P(B_{2})+P(A|B_{3})P(B_{3})$$
이를 총 확률의 법칙이라고 합니다. 이를 그림으로 도식화할 수 있습니다.
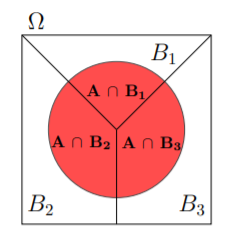
이때, 각각의 $B_{n}$은 서로 disjoint하고 $B_{n}$의 합집합이 표본 공간과 같다면 각각의 $B_{n}$을 분할(partition)이라고 합니다.
Ex2. 속이 보이지 않는 바구니에 5개의 빨간색 공, 그리고 2개의 초록색 공이 있고, 공을 순서대로 2개를 뽑는 다면 두번째 공이 빨간색 공이 되는 확률은?(이때, 처음에 뽑은 공은 다시 바구니에 넣지 않습니다.)
Answer
먼저, 표본 공간은 $\Omega={RR, RG, GR, GG}$가 됩니다. 여기서 R=빨간색 공, G=초록색 공 입니다.
이제 4가지 사건을 정의합니다.
$R_{1}$은 '첫번째 공이 빨간색'인 사건, $R_{2}$은 '두번째 공이 빨간색'인 사건, $G_{1}$은 '첫번째 공이 초록색'인 사건, $G_{2}$은 '두번째 공이 초록색'인 사건
따라서, 문제에서 저희가 구하고 싶은 확률은 $P(R_{2})=P(R_{2}|R_{1})P(R_{1})+P(R_{2}|G_{1})P(G_{1})$가 됩니다.
이를 계산하기 위해서는 $P(R_{2}|R_{1})$, $P(R_{1})$, $P(R_{2}|G_{1})$, $P(G_{1})$를 알아야합니다.
- $P(R_{2}|R_{1})$는 첫번째로 빨간색 공이 뽑힌것이 조건이므로 현재 바구니에는 6개 중에서 4개의 빨간색 공이 있습니다. 따라서 $\frac{4}{6}$입니다.
- $P(R_{2}|G_{1})$는 첫번째로 초록색 공이 뽑힌것이 조건이므로 현재 바구니에는 6개 중에서 5개의 빨간색 공이 있습니다. 따라서 $\frac{5}{6}$입니다.
- $P(R_{1})$는 첫번째로 빨간색 공을 뽑을 확률이므로 $\frac{5}{7}$입니다.
- $P(G_{1})$는 첫번째로 빨간색 공을 뽑을 확률이므로$\frac{2}{7}$입니다.
이제 최종 계산을 하게 되면$P(R_{2})=P(R_{2}|R_{1})P(R_{1})+P(R_{2}|G_{1})P(G_{1}) =\frac{4}{6}\frac{5}{7} + \frac{5}{6}\frac{2}{7}=\frac{5}{7}$가 되는 것을 알 수 있습니다.
***참고로 이 예제는 urn problem로 확률에서 자주 쓰이는 예시(동전 던지기) 중에 하나입니다. 관심 있으신 분은 한번씩 봐도 좋을 것 같습니다.(http://en.wikipedia.org/wiki/Urn_problem)
이번에는 좀 더 복잡한 예시를 설명하겠습니다. 하지만 urn problem의 범주에서는 벗어나지 않았습니다!!!
Ex3. 속이 보이지 않는 바구니에 5개의 빨간색 공, 그리고 2개의 초록색 공이 있습니다. 공을 뽑았을 때, 초록색 공이라면 바구니에 빨간색 공을 추가하고, 빨간색 공이라면 바구니에 초록색 공을 추가합니다.(이때, 처음에 뽑은 공은 다시 바구니에 넣지 않습니다.) 위와 같은 조건에서 두번째 공을 뽑았을 때, 두번째 공이 빨간색 공일 확률은?
Answer
Ex2와 동일하게 사건을 정의하면 저희가 구해야하는 것은 $P(R_{2})$이고, $P(R_{2}|R_{1})$, $P(R_{1})$, $P(R_{2}|G_{1})$, $P(G_{1})$를 알아야합니다.
여기서 중요한 점은 $P(R_{1})$, $P(G_{1})$는 어차피 처음에 뽑는 것이기 때문에 변하지 않고, $P(R_{2}|R_{1})$, $P(R_{2}|G_{1})$만
변한다는 점입니다.
- $P(R_{2}|R_{1})$,는 첫번째 공이 빨간색이므로 바구니에 초록색 공을 추가한 다음 다시 뽑을 때 빨간색 공이 나올 확률은 $\frac{4}{7}$입니다.
- $P(R_{2}|G_{1})$,는 첫번째 공이 초록색이므로 바구니에 빨간색 공을 추가한 다음 다시 뽑을 때 빨간색 공이 나올 확률은 $\frac{6}{7}$입니다.
이제 최종 계산을 하게 되면$P(R_{2})=P(R_{2}|R_{1})P(R_{1})+P(R_{2}|G_{1})P(G_{1}) =\frac{4}{7}\frac{5}{7} +\frac{6}{7}\frac{2}{7}=\frac{32}{49}$가 되는 것을 알 수 있습니다.
4. 조건부 확률의 구조화(트리화)
조건부 확률과 총 확률의 법칙을 계산하는 가장 좋은 방법은 사건들을 '트리(tree)화'시키는 것입니다. 나무를 뒤집은 것처럼 조건에 따라 서로 연결시킨 구조입니다.(트리 구조는 컴퓨터 공학의 자료구조 '트리'를 참고하시면 됩니다.)
이전에 했던 Ex4를 구조화시키면 아래의 그림과 같습니다.

- 위의 트리에서 각 점을 노드(node)라고 합니다.
- 각 노드가 연결된 선을 가지(branch)라고 합니다.
- 트리에서는 깊이를 표현할 때 레벨(level)이라고 합니다. 이때, 꼭대기 노드(top node)는 레벨이 0이고, 그 다음 노드는 레벨이 1로 깊어질 수록 레벨이 늘어납니다.
- 각 레벨의 노드들은 각 예제의 실험에서 나올 수 있는 경우 중 한가지를 표현합니다. 레벨 1에서는 첫번째 공을 뽑았을 때 가능한 경우, 레벨 2에서는 레벨 1의 조건하에 두 번째로 공을 뽑았을 때 가능한 경우를 의미합니다.
- 각 경우의 확률은 가지에 써집니다. 레벨 1에서 첫번째 공이 빨간색이 나올 확률은 $\frac{5}{7}$이고, 초록색이 나올 확률은 $\frac{2}{7}$가 됩니다. 레벨 2에서는 레벨 1의 조건하에 두 번째 공을 뽑았을 때 가능한 경우로 레벨 1에서 첫번째 공이 빨간색인 조건하에 레벨 2에서 두번째 공이 빨간색일 확률은 $\frac{4}{7}$입니다.
- 트리에서 조건부 확률에서의 곱셈 법칙은 어떤 노드에 도달할 확률로 그 경로를 따라가는 확률의 곱입니다. 즉, $P(R_{1} \cap R_{2})=P(R_{1})P(R_{2}|R_{1})=\frac{5}{7}\frac{4}{7}$가 됩니다.
- 트리에서 총 확률의 법칙은 마지막 노드가 같은 노드에 도달하기 위한 모든 경로에 따른 곱셉 법칙의 합입니다. 즉, $P(R_{2})=P(R_{1})P(R_{2}|R_{1})+P(G_{1})P(R_{2}|G_{1})=\frac{5}{7}\frac{4}{7}+\frac{2}{7}\frac{6}{7}=\frac{32}{49}$ 로 Ex4.의 답과 일치합니다.
5. 독립
두가지의 사건이 있을 때, 한 가지의 사건이 다른 사건에 영향을 주지 않는다면 두 사건은 서로 독립(independent)하다고 합니다.
예를 들어서 저희는 지금까지 동전을 2개를 던지는 경우 각 동전은 서로 영향을 주지 않는다고 암묵적으로 가정을 해왔습니다!! 하지만, 실제 확률 실험의 환경에서는 2가지의 동전이 독립적인 환경을 맞추기 위해 서로 부딪히게 던지지 않는 노력을 해야합니다.
정확하게 통제되어 독립된 실험을 통해 두 사건이 서로 영향을 주지 않는다면. 즉 $P(A|B)=P(A)$라면 사건 A와 사건 B는 서로 독립이라고 합니다. 이때, $P(A|B)=P(A)$가 의미하는 것은 사건 B가 사건 A에 영향을 주지 않기때문에 사건 B가 조건이더라도 사건 A는 영향을 받지 않기 때문에 서로 같게 됩니다.
- 독립 : 두 사건 A, B에 대해 $P(A \cap B)=P(A)P(B)$라면 A, B는 서로 독립(independent)이다.
독립의 정의에서 사용된 식은 조건부 확률을 통해 유도가능합니다. $P(A \cap B)=P(A|B)P(B)=P(A)P(B)$
당연하지만, 사건 A가 사건 B에 대해 독립적이라면 사건 B 역시 사건 A에 대해 독립적입니다. 이러한 성질을 대칭성(symmetry)라고 합니다.
위의 식을 사용해서 2가지 새로운 식을 유도할 수 있습니다.
1. $P(B) \neq 0$이라면 사건 A와 사건 B가 서로 독립일 조건은 $P(A|B)=P(A)$와 동치이다.
2. $P(A) \neq 0$이라면 사건 A와 사건 B가 서로 독립일 조건은 $P(B|A)=P(B)$와 동치이다.
Ex4. 같은 동전을 2번 던진다고 할 때, $H_{1}$을 첫번째 던졌을 때 앞면이 나오는 경우, $H_{2}$을 두번째 던졌을 때 앞면이 나오는 경우라고 하겠습니다. 이때, $H_{1}, H_{2}$는 서로 독립인지 판단하시오.
Answer
$H_{1} \cap H_{2}$는 두번 모두 앞면이 나오는 사건입니다. 따라서, $P(H_{1} \cap H_{2})=\frac{1}{4}=P(H_{1})P(H_{2})$이므로 두 사건은 독립입니다.
Ex5. 같은 동전을 3번 던진다고 할 때, $H_{1}$을 첫번째 던졌을 때 앞면이 나오는 경우, A을 앞면이 정확히 2번만 나오는 경우라고 하겠습니다. 이때, $H_{1}, A$는 서로 독립인지 판단하시오.
Answer
표본 공간을 나열한 뒤 A가 나올 확률을 계산하면 손쉽게 $P(A)=\frac{3}{8}$임을 알 수 있습니다.
이때, $H_{1}={HHH, HHT, HTH, HTT}$가 되고 $P(A|H_{1})=\frac{2}{4}$입니다. $P(A|H_{1}) \ne \frac{3}{8}$이므로 서로 독립이 아닙니다.
6. 베이지안 이론
드디어 베이지안 이론입니다. 베이지안에 대한 간단한 개념은 이전에 기초통계학[0](https://everyday-image-processing.tistory.com/5)에서 소개하였습니다.
베이지안 공식은 두 사건 A, B에 대해 $P(B|A)=\frac{P(A|B)P(B)}{P(A)}$입니다.
베이지안 공식이 우리에게 알려주는 것 중 한가지는 $P(A|B), P(B), P(A)$를 알고 있다면, 역 조건부 확률($P(B|A)$)을 알 수 있다는 것입니다.
Proof
베이지안 공식을 증명하기 위한 중요한 열쇠는 $P(A \cap B)$가 대칭성을 가진다는 점입니다. 따라서 $P(B|A)P(A)=P(A \cap B)=P(A|B)P(B)$ 입니다.
이 수식을 정리하면 베이지안 공식이 나오는 것을 볼 수 있습니다.
베이지안 이론은 이후에 통계 부분에서 굉장히 자세하게 다룰 예정이니 오늘은 간단하게 베이지안 공식이 무엇인지까지만 알아보고 여기서 마치도록 하겠습니다.
기초통계학[4].이산확률변수(https://everyday-image-processing.tistory.com/9)
'수학 > 기초통계학' 카테고리의 다른 글
| 기초통계학[5]. 이산확률변수의 기댓값 (0) | 2020.03.12 |
|---|---|
| 기초통계학[4].이산확률변수 (0) | 2020.03.08 |
| 기초통계학[2].확률 기초 (0) | 2020.03.05 |
| 기초통계학[1].경우의 수와 집합 (0) | 2020.03.03 |
| 기초통계학[0].소개 (0) | 2020.03.02 |
