안녕하세요. 오늘은 지난 시간의 기초통계학[22].베이즈 추론 5(https://everyday-image-processing.tistory.com/43)을 통해서 연속 사전확률과 연속 데이터를 가지는 경우에 베이즈 추론을 해보았습니다. 오늘은 지난 시간에 언급했듯이 사전확률분포가 주어져있지 않은 경우 어떻게 해야하는 지 알아보도록 하겠습니다.
먼저 공액 사전 확률분포는 사전 확률분포와 사후 확률분포가 동일한 분포를 가지는 경우의 사전 확률분포라고 하였습니다. 대표적으로 베타 분포와 정규 분포가 있기 때문에 2가지를 중심으로 알아보도록 하겠습니다. 좀 더 정확한 정의는 아래와 같습니다.
- 우도 $f(x|\theta)$를 가지는 데이터를 가지고, $\theta$에 대한 사전 확률분포 역시 모수 기반 분포라고 가정하면 $\theta$에 대한 사후 확률분포가 사전 확률분포의 족(family)에 속하면 사전 확률분포를 공액 사전 확률분포라고 한다.
1. 베타 분포(Beta Distribution)
지난 포스팅에서 봤던 베타 분석의 확률 밀도함수부터 상기하고 넘어가도록 하겠습니다.
$$f(\theta) = \frac{(a+b-1)!}{(a-1)!(b-1)!}\theta^{a-1}(1-\theta)^{b-1}$$
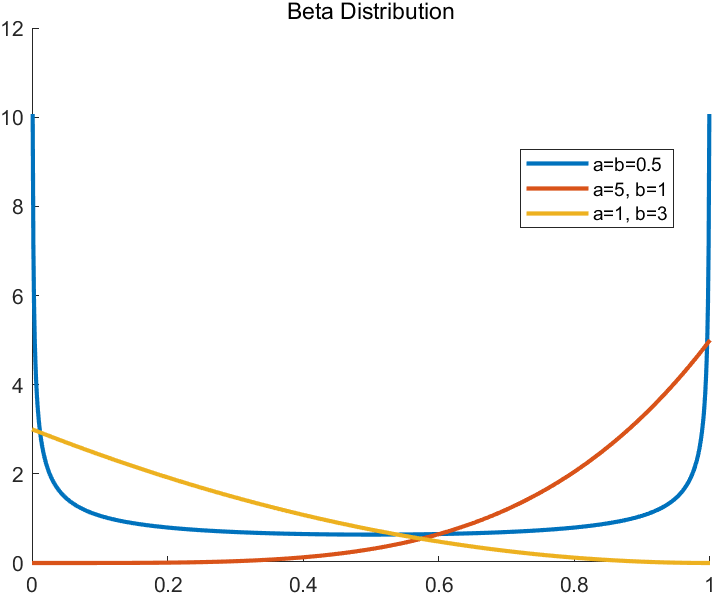
위 그림은 매트랩 함수를 통해 직접 그려본 베타 분포의 그림입니다. 이전 포스팅에서도 언급했다싶이 베타분포는 항상 $[0, 1]$ 사이의 정의역을 가지고 있습니다. 나머지 $[0, 1]$을 제외한 나머지 영역에서는 전부 0값을 가지고 있습니다. 이제부터 본격적으로 베타 분포가 이항 우도, 베르누이 우도, 기하 우도 공액 사전확률분포인지 확인해보도록 하겠습니다.
참고로 우도 함수가 이항 분포, 베르누이 분포일 때 사전 확률분포가 베타분포이면 사후 확률분포도 베타분포임을 확인해야합니다.
1.1. 이항 우도(Binomial likelihood)
먼저 이항 분포입니다. 데이터 $x$가 $x \sim {\sf Binomial}(N, \theta)$라고 가정해보겠습니다. 그러면 이항 분포에 대한 우도는 $f(x|\theta) = \frac{N!}{x!(N-x)!}\theta^{x}(1 - \theta)^{N-x}$입니다. 이는 간단하게 구할 수 있습니다. 그 다음으로 사전 확률분포가 베타 분포라고 가정하겠습니다. 따라서 $\theta$에 대한 사전 확률분포의 확률밀도함수는 $f(\theta) = \frac{(a+b-1)!}{(a-1)!(b-1)!}\theta^{a-1}(1-\theta)^{b-1}$입니다. 이제 사후 확률분포를 구할 수 있습니다. 계산이 조금 복잡하니 단계를 나눠서 진행해보겠습니다.
1). 우도와 사전확률을 곱합니다. 그러면 $f(x|\theta) \cdot f(\theta) = \frac{(a+b-1)!}{(a-1)!(b-1)!}\frac{N!}{x!(N-x)!}\theta^{(a-1)+x}(1 - \theta)^{(b-1) + (N - x)}$입니다.
2). 이제 사전확률분포의 총 확률 법칙을 사용해서 1)에서 구한 식을 나누어줍니다. $f(x) = \int_{0}^{1} f(x|\theta) \cdot f(\theta) \; d\theta$를 계산하면 됩니다. 그런데 적분해야하는 식이 만만치 않습니다. 어떻게 해결해야 할까요? 바로 베타 함수(Beta function)을 사용하는 것입니다. 베타 함수식을 보면 주어진 식은 전형적인 베타 함수임을 쉽게 알 수 있습니다.
$$B(a+1, b+1) = \int_{0}^{1} x^{a} (1-x)^{b} \; dx = \frac{\Gamma(a+1)\Gamma(b+1)}{\Gamma(a+b+2)} = \frac{a!b!}{(a+b+1)!}$$
따라서 식을 적당히 조작하여 $f(x) = \frac{(a+b-1)!}{(a-1)!(b-1)!}\frac{N!}{x!(N-x)!}\frac{(a+x-1)!(b+N-x+1)!}{(a+b+N-1)!}$을 얻을 수 있습니다. 이제 마지막으로 $f(x)$를 $f(x|\theta) \cdot f(\theta)$에 나누어주면 됩니다.
근데 어차피 앞에 붙은 2개의 계수는 동일하므로 최종적으로 $f(\theta|x) =\frac{(a+b+N-1)!}{(a+x-1)!(b+N-x+1)!}\theta^{a+x-1}(1-\theta)^{b+N-x-1}$입니다.
이때, $f(\theta|x)$는 $Beta(a+x, b+N-x)$와 동일하다는 것을 생각해보면 사후 확률분포 역시 베타 분포임을 알 수 있습니다. 다만 사전 확률분포의 베타 분포와 모수만 다를 뿐입니다. 즉, 같은 베타 분포 족인 것이죠.
따라서 이항 분포일 때 우도의 베타 분포는 공액 사전확률임을 알 수 있습니다.
앞으로 베타 분포의 계수를 계속 사용할 예정이니 그냥 $c_{1}$이라고 하겠습니다. 참고로 어차피 사후 확률분포의 확률 밀도함수의 계수 역시 사전 확률분포의 계수와 우도의 계수가 없어지고 새로운 베타 분포의 계수를 계속 얻을 수 있음을 알아주셨으면 좋겠습니다.
1.2. 베르누이 우도(Bernoulli likelihood)
이항 분포 때와 동일하게 확인할 수 있습니다. 먼저 베르누이 분포는 경우의 수를 $x=0$과 $x=1$ 2가지로 나눌 수 있습니다. $x=1$인 경우부터 사후 확률분포를 구해보겠습니다. 현재 베르누이 분포를 다루고 있기 때문에 $x=1$인 경우의 우도는 $f(x|\theta)=\theta$임을 알 수 있습니다.
이때 사후 확률분포는 $f(x|\theta) \cdot f(\theta)$를 $f(x)$로 나누어주면 됩니다. $f(x|\theta) \cdot f(\theta) = c_{1}\theta^{a}(1-\theta)^{b-1}$이고 $f(x) = c_{1}\int_{0}^{1} \theta^{a}(1-\theta) \; d\theta$는 방금 봤던 베타 함수를 사용해서 표현하면 $\frac{a!(b-1)!}{(a+b)!}$임을 쉽게 알 수 있습니다. 따라서 $f(\theta|x) = \frac{(a+b)!}{a!(b-1)!}\theta^{a}(1-\theta)^{b-1}$이고 이는 $beta(a+1, b)$입니다.
이제 $x=0$인 경우를 살펴보면 다른 점은 $beta(a, b+1)$이라는 점입니다.
따라서 베르누이 분포일 때 우도의 베타 분포는 공액 사전확률임을 알 수 있습니다.
'수학 > 기초통계학' 카테고리의 다른 글
| 기초통계학[25].공액 사전 확률분포 선택 (0) | 2020.06.30 |
|---|---|
| 기초통계학[24].공액 사전 확률분포 2 (0) | 2020.04.27 |
| 기초통계학[22].베이즈 추론 5 - 연속 사전확률과 연속 데이터를 가지는 경우에 대하여 (0) | 2020.04.17 |
| 기초통계학[21]. 베타 분포(Beta Distribution) (0) | 2020.04.15 |
| 기초통계학[20].베이즈 추론 4 - 연속 사전확률을 가지는 경우에 대하여 (0) | 2020.04.12 |
안녕하세요. 오늘은 지난 시간의 기초통계학[22].베이즈 추론 5(https://everyday-image-processing.tistory.com/43)을 통해서 연속 사전확률과 연속 데이터를 가지는 경우에 베이즈 추론을 해보았습니다. 오늘은 지난 시간에 언급했듯이 사전확률분포가 주어져있지 않은 경우 어떻게 해야하는 지 알아보도록 하겠습니다.
먼저 공액 사전 확률분포는 사전 확률분포와 사후 확률분포가 동일한 분포를 가지는 경우의 사전 확률분포라고 하였습니다. 대표적으로 베타 분포와 정규 분포가 있기 때문에 2가지를 중심으로 알아보도록 하겠습니다. 좀 더 정확한 정의는 아래와 같습니다.
- 우도 $f(x|\theta)$를 가지는 데이터를 가지고, $\theta$에 대한 사전 확률분포 역시 모수 기반 분포라고 가정하면 $\theta$에 대한 사후 확률분포가 사전 확률분포의 족(family)에 속하면 사전 확률분포를 공액 사전 확률분포라고 한다.
1. 베타 분포(Beta Distribution)
지난 포스팅에서 봤던 베타 분석의 확률 밀도함수부터 상기하고 넘어가도록 하겠습니다.
$$f(\theta) = \frac{(a+b-1)!}{(a-1)!(b-1)!}\theta^{a-1}(1-\theta)^{b-1}$$

위 그림은 매트랩 함수를 통해 직접 그려본 베타 분포의 그림입니다. 이전 포스팅에서도 언급했다싶이 베타분포는 항상 $[0, 1]$ 사이의 정의역을 가지고 있습니다. 나머지 $[0, 1]$을 제외한 나머지 영역에서는 전부 0값을 가지고 있습니다. 이제부터 본격적으로 베타 분포가 이항 우도, 베르누이 우도, 기하 우도 공액 사전확률분포인지 확인해보도록 하겠습니다.
참고로 우도 함수가 이항 분포, 베르누이 분포일 때 사전 확률분포가 베타분포이면 사후 확률분포도 베타분포임을 확인해야합니다.
1.1. 이항 우도(Binomial likelihood)
먼저 이항 분포입니다. 데이터 $x$가 $x \sim {\sf Binomial}(N, \theta)$라고 가정해보겠습니다. 그러면 이항 분포에 대한 우도는 $f(x|\theta) = \frac{N!}{x!(N-x)!}\theta^{x}(1 - \theta)^{N-x}$입니다. 이는 간단하게 구할 수 있습니다. 그 다음으로 사전 확률분포가 베타 분포라고 가정하겠습니다. 따라서 $\theta$에 대한 사전 확률분포의 확률밀도함수는 $f(\theta) = \frac{(a+b-1)!}{(a-1)!(b-1)!}\theta^{a-1}(1-\theta)^{b-1}$입니다. 이제 사후 확률분포를 구할 수 있습니다. 계산이 조금 복잡하니 단계를 나눠서 진행해보겠습니다.
1). 우도와 사전확률을 곱합니다. 그러면 $f(x|\theta) \cdot f(\theta) = \frac{(a+b-1)!}{(a-1)!(b-1)!}\frac{N!}{x!(N-x)!}\theta^{(a-1)+x}(1 - \theta)^{(b-1) + (N - x)}$입니다.
2). 이제 사전확률분포의 총 확률 법칙을 사용해서 1)에서 구한 식을 나누어줍니다. $f(x) = \int_{0}^{1} f(x|\theta) \cdot f(\theta) \; d\theta$를 계산하면 됩니다. 그런데 적분해야하는 식이 만만치 않습니다. 어떻게 해결해야 할까요? 바로 베타 함수(Beta function)을 사용하는 것입니다. 베타 함수식을 보면 주어진 식은 전형적인 베타 함수임을 쉽게 알 수 있습니다.
$$B(a+1, b+1) = \int_{0}^{1} x^{a} (1-x)^{b} \; dx = \frac{\Gamma(a+1)\Gamma(b+1)}{\Gamma(a+b+2)} = \frac{a!b!}{(a+b+1)!}$$
따라서 식을 적당히 조작하여 $f(x) = \frac{(a+b-1)!}{(a-1)!(b-1)!}\frac{N!}{x!(N-x)!}\frac{(a+x-1)!(b+N-x+1)!}{(a+b+N-1)!}$을 얻을 수 있습니다. 이제 마지막으로 $f(x)$를 $f(x|\theta) \cdot f(\theta)$에 나누어주면 됩니다.
근데 어차피 앞에 붙은 2개의 계수는 동일하므로 최종적으로 $f(\theta|x) =\frac{(a+b+N-1)!}{(a+x-1)!(b+N-x+1)!}\theta^{a+x-1}(1-\theta)^{b+N-x-1}$입니다.
이때, $f(\theta|x)$는 $Beta(a+x, b+N-x)$와 동일하다는 것을 생각해보면 사후 확률분포 역시 베타 분포임을 알 수 있습니다. 다만 사전 확률분포의 베타 분포와 모수만 다를 뿐입니다. 즉, 같은 베타 분포 족인 것이죠.
따라서 이항 분포일 때 우도의 베타 분포는 공액 사전확률임을 알 수 있습니다.
앞으로 베타 분포의 계수를 계속 사용할 예정이니 그냥 $c_{1}$이라고 하겠습니다. 참고로 어차피 사후 확률분포의 확률 밀도함수의 계수 역시 사전 확률분포의 계수와 우도의 계수가 없어지고 새로운 베타 분포의 계수를 계속 얻을 수 있음을 알아주셨으면 좋겠습니다.
1.2. 베르누이 우도(Bernoulli likelihood)
이항 분포 때와 동일하게 확인할 수 있습니다. 먼저 베르누이 분포는 경우의 수를 $x=0$과 $x=1$ 2가지로 나눌 수 있습니다. $x=1$인 경우부터 사후 확률분포를 구해보겠습니다. 현재 베르누이 분포를 다루고 있기 때문에 $x=1$인 경우의 우도는 $f(x|\theta)=\theta$임을 알 수 있습니다.
이때 사후 확률분포는 $f(x|\theta) \cdot f(\theta)$를 $f(x)$로 나누어주면 됩니다. $f(x|\theta) \cdot f(\theta) = c_{1}\theta^{a}(1-\theta)^{b-1}$이고 $f(x) = c_{1}\int_{0}^{1} \theta^{a}(1-\theta) \; d\theta$는 방금 봤던 베타 함수를 사용해서 표현하면 $\frac{a!(b-1)!}{(a+b)!}$임을 쉽게 알 수 있습니다. 따라서 $f(\theta|x) = \frac{(a+b)!}{a!(b-1)!}\theta^{a}(1-\theta)^{b-1}$이고 이는 $beta(a+1, b)$입니다.
이제 $x=0$인 경우를 살펴보면 다른 점은 $beta(a, b+1)$이라는 점입니다.
따라서 베르누이 분포일 때 우도의 베타 분포는 공액 사전확률임을 알 수 있습니다.
'수학 > 기초통계학' 카테고리의 다른 글
| 기초통계학[25].공액 사전 확률분포 선택 (0) | 2020.06.30 |
|---|---|
| 기초통계학[24].공액 사전 확률분포 2 (0) | 2020.04.27 |
| 기초통계학[22].베이즈 추론 5 - 연속 사전확률과 연속 데이터를 가지는 경우에 대하여 (0) | 2020.04.17 |
| 기초통계학[21]. 베타 분포(Beta Distribution) (0) | 2020.04.15 |
| 기초통계학[20].베이즈 추론 4 - 연속 사전확률을 가지는 경우에 대하여 (0) | 2020.04.12 |
