안녕하세요. 오늘은 지난 포스팅의 [IC2D] Going Deeper with Convolutions (CVPR2015)에서 소개드린 GooLeNet에 이어 ILSVRC 2015에서 VGGNet과 GoogLeNet을 압도적인 차이로 이긴 ResNet을 소개해드리도록 하겠습니다. ResNet은 현재 Semantic Segmentation, Object Detection과 같은 비전 분야에서 필수적으로 사용되고 있는 기본 모델로써 알고 사용하는 것이 굉장히 중요합니다. 오늘은 ResNet을 개발하게 된 동기를 이해한다면 쉽게 이해할 수 있습니다.
Deep Residual Learning for Image Recognition
Deeper neural networks are more difficult to train. We present a residual learning framework to ease the training of networks that are substantially deeper than those used previously. We explicitly reformulate the layers as learning residual functions with
arxiv.org
배경
VGGNet에서 주요 쟁점은 네트워크의 깊이는 모델의 성능에 가장 큰 영향을 미친다는 것을 밝혔습니다. 그렇다면 한가지 궁금점이 생기겠죠? 그럼 하드웨어가 허락하는 만큼 무조건 더 깊게 네트워크를 구성하면 성능이 항상 좋아질까라는 의문점입니다. 하지만, 여기에는 당연하게도 몇 가지 문제점이 존재합니다.
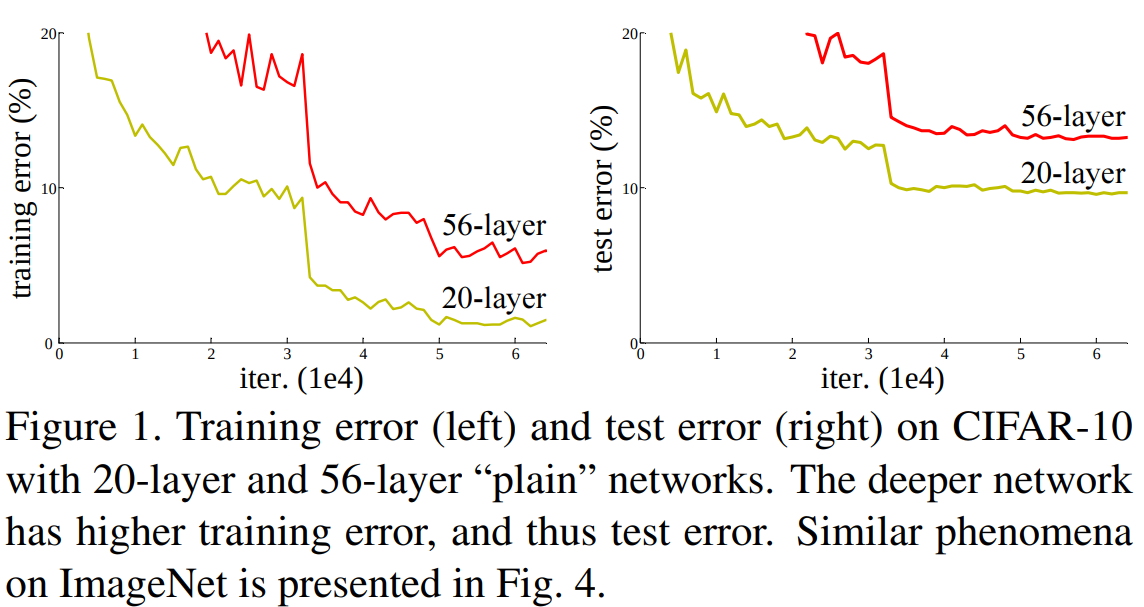
본 논문에서는 먼저 위 그림을 보여주고 있습니다. 네트워크의 깊이는 2배 가량 더 깊어졌지만 성능은 오히려 훨씬 떨어진것을 볼 수 있습니다. 여기서 사용한 네트워크는 Plain CNN으로 VGGNet과 같이 그냥 연속적으로 여러 개의 합성곱 계층을 추가한 모델입니다. 결과는 Training / Test error 모두 크게 차이가 나는 것을 볼 수 있죠. 왜 그럴까요?
일반적으로 Training error는 낮지만 Test error가 높은 현상을 과적합 (overfitting)이라고 하지만 Figure 1에서는 둘 다 낮기 때문에 과적합이라고 보기는 어렵습니다. 본 논문에서는 이러한 현상을 설명할 수 있는 것은 2가지 문제로 보고 있습니다. 첫번째는 Gradient Vanishing Problem과 Degradation Problem입니다.
먼저, Gradient Vanishing Problem은 너무 깊은 네트워크를 구성하는 경우 손실함수의 기울기가 얕은 계층까지 전달되지 못하고 소실되는 현상을 의미합니다. 이를 해결하기 위해서는 중간에 배치 정규화 (Batch Normalization) 등을 추가함으로써 어느정도 해결할 수 있습니다. 다음 문제인 Degradation Problem은 Gradient Vanishing Problem과는 다른 문제로 네트워크 깊이가 깊어지면 특정 깊이에서 어느순간 성능이 급감하는 현상을 의미합니다. 이러한 Degradation Problem을 해결하기 위해서는 깊은 모델을 위한 새로운 최적화 알고리즘을 개발하거나 기존의 최적화 알고리즘에서도 잘 동작하는 새로운 깊은 모델을 개발하는 것입니다. 본 논문에서는 새로운 모델을 개발하는 데 목표를 세우게 되죠. 따라서 본 논문의 목표는 깊은 모델을 만들었을 때 Degradation Problem이 없는 모델을 만드는 것이 목표이죠.
Residual Network
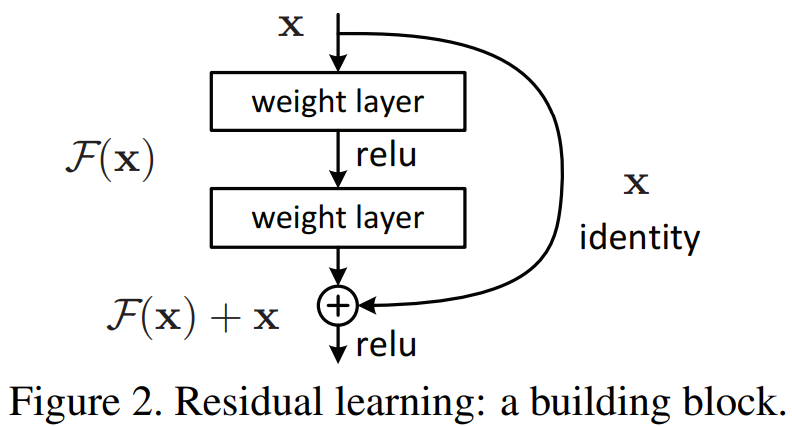
본 논문에서는 이를 해결하기 위해 Residual Block이라는 새로운 구조의 네트워크 블럭을 구현하였습니다. 방식은 아주 단순합니다. 입력 특징맵을 $\mathbf{x}$라고 두고 합성곱 블럭을 $\mathcal{F}$라고 하면 Residual Block의 출력은 $\mathcal{F}(\mathbf{x}) + \mathbf{x}$가 됩니다. 즉, 단순히 기존의 출력 특징맵에 입력 특징맵을 더해주는 것 입니다. 이제 여기에 ReLU까지 적용한 결과를 $\mathcal{H}$라고 두면 $\mathcal{H}(\mathbf{x}) = \mathcal{\mathbf{x}} + \mathbf{x}$라고 할 수 있습니다. 이와 같이 중간에 블럭을 건너뛰고 출력 특징맵에 입력 특징맵을 더해주는 연결을 Skip Connection이라고 부릅니다.
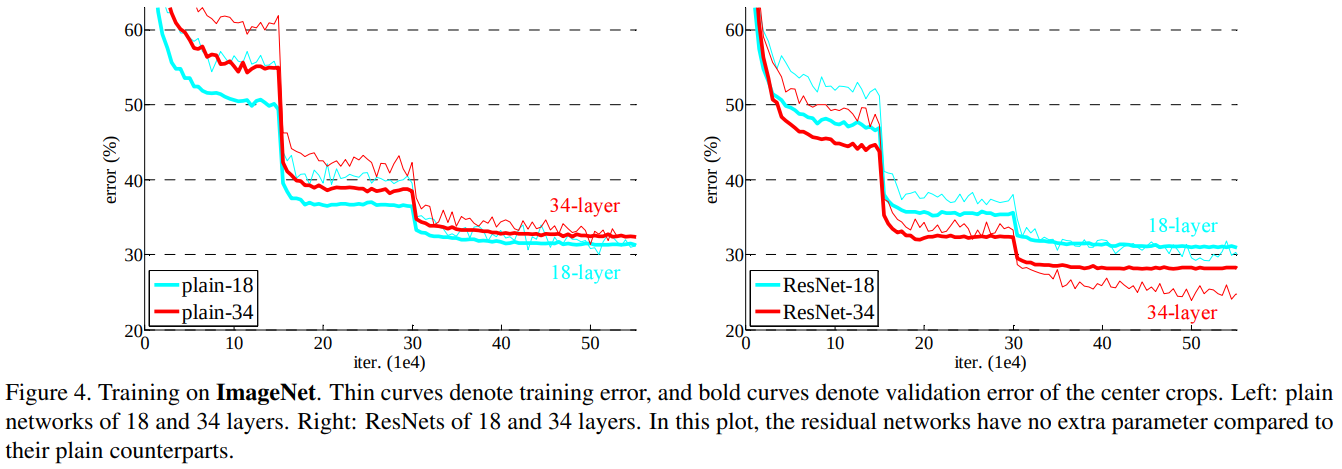
Figure 4에서 왼쪽은 Plain CNN, 오른쪽은 ResNet으로 각각 18개, 34개의 계층으로 구성한 네트워크의 ImageNet 학습 결과입니다. 실험 결과는 놀랍게도 기존의 Plain CNN이 가지고 있던 Degradation Problem이 없어지고 깊어질수록 그 성능이 향상된 것을 볼 수 있습니다.
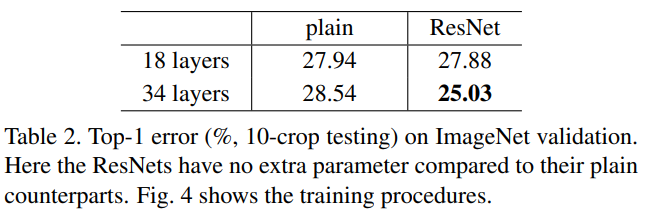
Table 2에서는 수치적으로 18 layer에 비해 34 layer에서 2.85%의 성능 향상을 얻게 되었습니다.
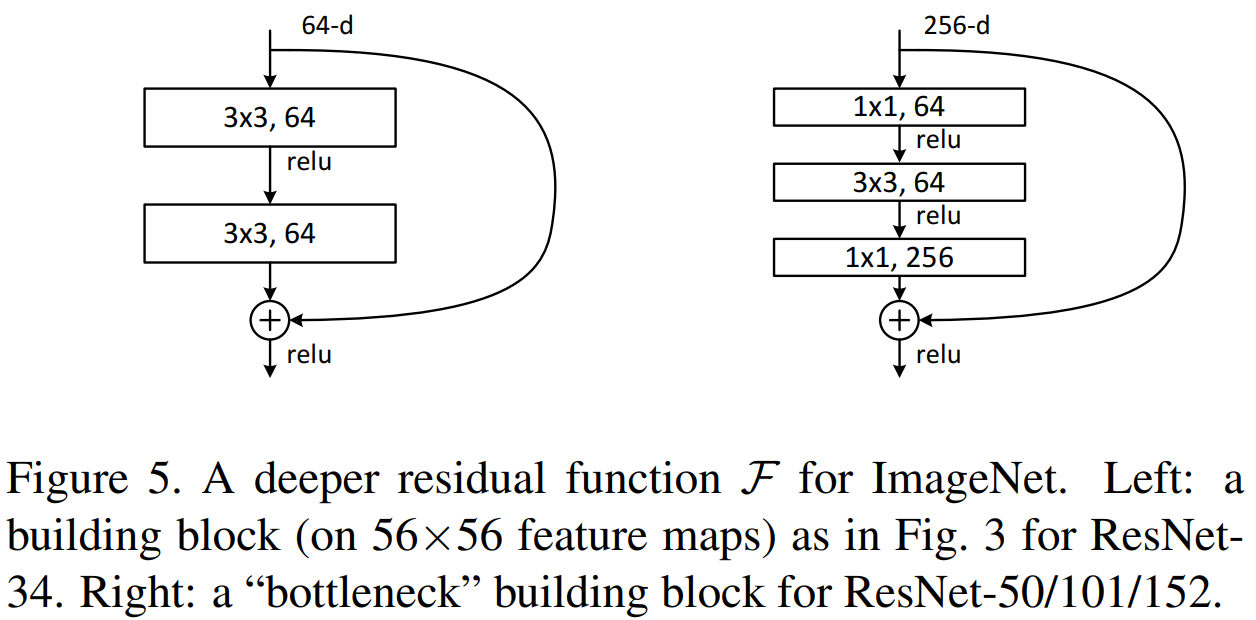
하지만, 네트워크가 깊어질수록 그 연산량이 보다 커지기 때문에 본 논문에서는 이를 해결하고자 50층 이상의 ResNet에서는 Bottleneck Block을 추가하였습니다. Figure 5의 왼쪽은 Basic Block으로 Bottleneck Block과의 가장 큰 차이점은 3개의 합성곱 계층을 사용하며 $1 \times 1$ 합성곱 필터 크기를 사용하여 연산량을 줄였다는 점 입니다. 이를 통해, 더욱 많은 비선형성이 도입되기 때문에 더욱 다양한 특징 맵을 얻을 수 있다는 장점이 있죠.
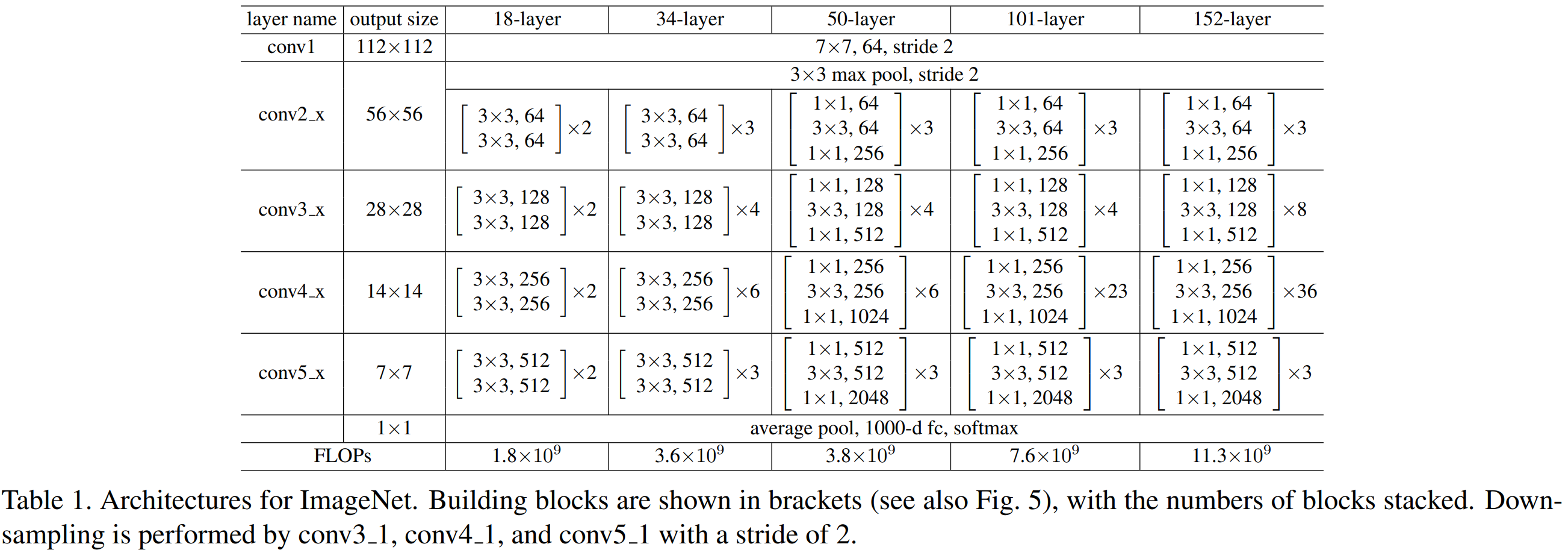
Table 1은 ResNet을 18층, 34층, 50층, 101층, 152층으로 나누어 구현한 모습입니다. 모든 모델은 공통적으로 $7 \times 7$ 크기의 필터를 적용하여 기초적으로 특징맵을 뽑아내게 됩니다.
Implementation Details
이번에는 ResNet의 전체 코드를 분석해보는 시간을 갖도록 하겠습니다.
class ResNet(nn.Module) :
def __init__(self, block, num_block, num_classes=100, num_channels=3):
super(ResNet, self).__init__()
self.in_channels = 64
self.conv1 = nn.Sequential(
nn.Conv2d(num_channels, 64, kernel_size=(3, 3), padding=(1, 1), bias=False),
nn.BatchNorm2d(64),
nn.ReLU()
)
self.conv2_x = self._make_layer(block, 64, num_block[0], 1)
self.conv3_x = self._make_layer(block, 128, num_block[1], 2)
self.conv4_x = self._make_layer(block, 256, num_block[2], 2)
self.conv5_x = self._make_layer(block, 512, num_block[3], 2)
self.avg_pool = nn.AdaptiveAvgPool2d((1, 1))
self.fc = nn.Linear(512 * block.expansion, num_classes)
def _make_layer(self, block, out_channels, num_blocks, stride):
strides = [stride] + [1] * (num_blocks - 1)
layers = []
for stride in strides :
layers.append(block(self.in_channels, out_channels, stride))
self.in_channels = out_channels * block.expansion
return nn.Sequential(*layers)
def forward(self, x):
output = self.conv1(x)
output = self.conv2_x(output)
output = self.conv3_x(output)
output = self.conv4_x(output)
output = self.conv5_x(output)
output = self.avg_pool(output)
output = output.view(output.size(0), -1)
output = self.fc(output)
return output
기본적으로 모든 ResNet은 stem_convolution을 가지고 있으며 해당 계층에서 일차적으로 특징 맵을 추출하게 됩니다. 다음으로는 Table 1에서 보시다싶이 ResNet의 깊이에 따라 BasicBlock 또는 BottleNeck Block의 개수가 달라지는 것을 볼 수 있습니다. 예를 들어, ResNet-18의 경우 BasicBlock을 각 stage에서 [2, 2, 2, 2] 만큼 사용하게 됩니다. ResNet-50에서는 BottleNeck Block을 각 stage에서 [3, 4, 6, 3]만큼 사용하게 되죠. 여기까지는 Table 1에 명시된 내용을 그대로 따라하기 때문에 어렵지 않습니다.
class BasicBlock(nn.Module) :
"""Basic Block for resnet 18 and resnet 34
"""
#BasicBlock and BottleNeck block
#have different output size
#we use class attribute expansion
#to distinct
expansion = 1
def __init__(self, in_channels, out_channels, stride=1):
super(BasicBlock, self).__init__()
# residual function
self.residual_function = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=(3, 3), stride=(stride, stride), padding=(1, 1), bias=False),
nn.BatchNorm2d(out_channels), nn.ReLU(inplace=True),
nn.Conv2d(out_channels, out_channels * BasicBlock.expansion, kernel_size=(3, 3), padding=(1, 1), bias=False),
nn.BatchNorm2d(out_channels * BasicBlock.expansion)
)
# shortcut
self.shortcut = nn.Sequential()
#the shortcut output dimension is not the same with residual function
#use 1*1 convolution to match the dimension
if stride != 1 or in_channels != BasicBlock.expansion * out_channels :
self.shortcut = nn.Sequential(
nn.Conv2d(in_channels, out_channels * BasicBlock.expansion, kernel_size=(1, 1), stride=(stride, stride), bias=False),
nn.BatchNorm2d(out_channels * BasicBlock.expansion)
)
def forward(self, x):
return nn.ReLU(inplace=True)(self.residual_function(x) + self.shortcut(x))
BasicBlock 역시 특별하게 어려운 부분은 없습니다. Table 1과 마찬가지로 $3 \times 3$ 합성곱을 2번 쓰는 것을 볼 수 있죠. 다만, ResNet에서 가장 중요한 특징인 Skip Connection이 여기서 처음 등장합니다. 저희가 Skip Connection을 하게 되면 기본적으로 원소별 덧셈 (element-wise summation)을 해야합니다. 이를 위해서는 더해지는 두 특징맵의 모양이 완벽하게 동일해야하죠. 만약, 해상도 또는 채널의 개수 중 하나라도 다르다면 shape 관련 에러가 발생할 것 입니다. 여기서 if 문이 해당 문제를 보완해주고 있죠.
첫번째 조건은 stride != 1 인 경우 입니다. 일반적으로 $H_{i}$의 높이를 가지는 특징맵이 패딩 $P$ 그리고 필터의 크기가 $F$인 합성곱을 stride $S$를 통과하게 되면 출력 특징맵의 높이 $H_{o}$ 사이의 관계는 다음과 같습니다.
$$H_{o} = \frac{H_{i} + 2P - F}{S} + 1$$
위 코드에서는 $P = 1$ 그리고 $F = 3$이므로 출력 특징맵의 높이는 $H_{o} = \frac{H_{i} - 1}{S} + 1$임을 알 수 있습니다. 이때, $S = 1$이라면 $H_{o} = (H_{i} - 1) + 1 = H_{i}$이므로 입력 특징맵과 동일한 높이를 가지게 됩니다. 하지만, $S \neq 1$이라면 두 특징맵의 크기는 다르기 때문에 shape 에러가 나올 것 입니다. 즉, 첫번째 조건문은 해상도가 안맞는 경우를 해결하고자 하는 것이죠.
두번째 조건은 in_channels != BasicBlock.expansion * out_channels로 이름에서도 느껴지다 싶이 해당 조건문은 두 특징맵의 채널 크기가 다른 경우를 다루기 위해 추가되었습니다. 따라서, 이 두 조건을 통해 해상도과 채널의 개수가 모두 동일해지도록 shortcut의 출력 특징맵을 조절하는 것이죠.
class BottleNeck(nn.Module):
"""Residual block for resnet over 50 layers
"""
expansion = 4
def __init__(self, in_channels, out_channels, stride=1):
super().__init__()
self.residual_function = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=1, bias=False),
nn.BatchNorm2d(out_channels), nn.ReLU(inplace=True),
nn.Conv2d(out_channels, out_channels, stride=stride, kernel_size=3, padding=1, bias=False),
nn.BatchNorm2d(out_channels), nn.ReLU(inplace=True),
nn.Conv2d(out_channels, out_channels * BottleNeck.expansion, kernel_size=1, bias=False),
nn.BatchNorm2d(out_channels * BottleNeck.expansion),
)
self.shortcut = nn.Sequential()
if stride != 1 or in_channels != out_channels * BottleNeck.expansion:
self.shortcut = nn.Sequential(
nn.Conv2d(in_channels, out_channels * BottleNeck.expansion, stride=stride, kernel_size=1, bias=False),
nn.BatchNorm2d(out_channels * BottleNeck.expansion)
)
def forward(self, x):
return nn.ReLU(inplace=True)(self.residual_function(x) + self.shortcut(x))
마지막으로 BottleNeck Block입니다. 해당 Block은 BasicBlock과 거의 동일하며 다른 점은 $1 \times 1$ 크기의 합성곱 계층을 2번, 중간에 $3 \times 3$ 크기의 합성곱 계층을 1번 사용하여 계산상의 이점을 얻었다는 것 입니다.
'논문 함께 읽기 > 2D Image Classification (IC2D)' 카테고리의 다른 글
| [IC2D] Deep Networks with Stochastic Depth (ECCV2016) (0) | 2023.05.03 |
|---|---|
| [IC2D] Identity Mappings in Deep Residual Networks (ECCV2016) (0) | 2023.04.21 |
| [IC2D] Going Deeper with Convolutions (CVPR2015) (0) | 2023.02.17 |
| [IC2D] Very Deep Convolutional Networks for Large-Scale Image Recognition (ICLR2015) (0) | 2023.02.17 |
| 2D Image Classification Summary (0) | 2023.02.17 |
