안녕하세요. 오늘은 CVPR 2019에 MIT에서 나온 Data augmentation using learned transformations for one-shot medical image segmentation입니다. 논문 출처는 https://arxiv.org/pdf/1902.09383.pdf 입니다. 코드는 https://github.com/xamyzhao/brainstorm 에 있으니 참고하시길 바랍니다.(조만간 코드 분석 포스팅도 올리겠습니다.)
혹시 method부터 보고 싶으신 분은 넘어가시면 됩니다.
0. Abstract
image segmentation은 medical에서 중요한 분야 중 하나입니다. 최근들어 CNN 기반 image segmentation은 SOTA(state-of-the-art) 성능을 내고 있습니다. 하지만 일반적으로 supervised learning 기반으로 구현하려면 labeling된 큰 dataset을 필요로 합니다. 또한 dataset을 labeling하는 것조차 많은 전문가와 시간을 필요로 합니다. 이런 상황에서 일반적인 data augmentation을 적용하게 되면 medical image에서 복잡한 변화을 잡지 못하게 되므로 새로운 방법이 필요합니다.
본 논문에서는 labeling된 medical image를 새로 만들기(synthesizing)위한 자동화된(automated) data augmentation 기법을 제안합니다. 제안 방식의 유효성을 뇌 종양 MRI dataset을 통해서 진행하게 됩니다.
본 논문에서 중요한 차이점은 오직 1개의 segmented(labeled) scan image가 필요하고 다른 unsegmented(labeled) scan image는 semi-supervised learning을 통해 해결합니다. 이때 1개의 segmented(labeled) scan image을 통해 모델이 transformation을 학습하게 됩니다. 그 모델을 이용해서 labeled imgae를 통해서 새로운 labeled examples(sythesized images)를 얻습니다. 여기서 각각의 transformation은 spatial deformation, intensity change로 구성되어 복잡한 변화를 잡을 수 있게 됩니다.
1. Introduction
Semantic image segmentation은 biomedical image 분야에서 핵심입니다. 활용 분야로는 세포 분포 분석, 진단학, 치료 계획 설정 등이 있습니다. 실제로 충분한 양의 labeled data가 존재한다면 supervised deep learning은 SOTA 성능을 내고 있습니다. 하지만 일반적으로 medical image의 label을 얻는 것은 상당한 시간과 노력이 들어가게 됩니다. 대부분은 치료 영상 datase에서 label이 있는 data는 굉장히 적습니다. 이러한 labeled data 부족 문제는 실제로 비교할 label이 없기 때문에 예측된 label과 직관적으로 보는 label 사이의 차이를 더 악화시키는 결과를 가져오게 됩니다.
이런 data 부족 문제를 해결하기 위해서 많은 supervised 생물의료학 segmentation 기법들은 network의 구조와 전문가들이나 프로그래머들이 preprocessing에 집중하는 방향으로 발전하였습니다. 이는 물론 training data의 크기를 늘리기 위한 data augmentation도 포함됩니다. 대표적인 data augmentation transformation 함수로는 random image rotation, random nonlinear deformation이 있습니다. 이들은 구현도 쉬워서 자주 사용되는 방법입니다. 또한 segmentation 성능을 올리는 데도 효과가 있습니다! 하지만 이들은 parameter에 민감하고 새로운 data가 추가되었을 때 변화를 감지하는 능력도 떨어지게 됩니다.
본 논문에서는 data에 비해 label이 부족한 문제를 다양하고 진짜같은 labeled example을 합성하는 것을 학습함으로서 해결하고자 합니다. 본 논문에서 제시하는 자동화된 data augmentation은 unlabeled data와의 연결점을 찾도록 합니다. learning-based registration을 사용하여 dataset의 image 사이의 spatial transformation과 appearance(intensity) transformation의 set들을 모델링합니다. 이 모델은 unlabeled data에서 해부학적(anatomical) 다양성과 image 다양성을 capture합니다. dataset에서 image를 sampling함으로서 얻는 sampling transformation과 이를 single labeld example에 적용함으로서 새로운 example을 얻게 됩니다.
이 방법이 효과 있음을 뇌 종양 MRI의 one-shot segmentation을 통해 증명하게 됩니다. 비교하는 대상으로 SOTA 성능을 가지는 one-shot biomedical segmentation들과 비교하게 됩니다. 대표적으로 single-atlas segmentation, 기존의 data augmentation을 이용한 supervised segmentation입니다.
2. Related work
2.1. Medical image segmentation
본 논문에서는 뇌종양 MRI의 segmentation에 집중합니다. 하지만 뇌종양 MRI의 경우 해결하기 어려운 몇 가지 문제점들이 있습니다. 먼저, 사람의 뇌는 해부학적으로 중요한 변화가 존재합니다. 그리고, MRI의 intensity는 특정 noise, 스캐너의 protocol과 quality, 뿐만 아니라 다양한 image parameter에 따라 다양합니다. 이는 tissue(조직) class에서 같은 MRI 장비라도 MRI를 통해 얻은 image들 끼리 서로 다른 intensity를 나타낼 수 있다라는 것을 의미합니다.
많은 segmentation 기법들은 이러한 intensity-related 문제를 완화하기 위해서 스캔 preprocessing에 의존하고 있습니다. preprocessing 기법은 활용하는 데 비용도 많이 들고 현재도 많이 연구되는 분야입니다. 본 논문에서의 augmentation 기법은 이 문제를 다른 관점으로 해결하려합니다. 즉, intensity의 variation을 없애는 방법을 사용하지 않고 MRI scan에서 실제 image intensity variation에 있어 더 robust하게 만드는 방법을 강구합니다.
전통적인 segmentation method로 atlas-based(atlas-guided) segmentation이 있습니다. 이는 현재 참조하는 labeled data의 deformation model을 사용하여 target data에 registration을 수행하고 그에 대응되는 label 역시 동일한 model을 사용해서 registration을 수행합니다. multiple-atlas가 사용가능하면 labeled된 각각의 class 사이의 해부학적 분포는 deformation model에 의해서 capture될 것입니다. 그리고 intensity variation의 경우 preprocessed scan을 사용하거나 normalized cross-correlation과 같은 intensity-robust metric을 이용해서 완화하게 됩니다. 하지만 tissue의 외형(본 논문에서는 appearance로 쓰였으며, intensity와 같은 말로 해석할 수 있습니다.)의 모호함(tissue간 불명확한 경계, image noise 등등...)은 여전히 registration과 segmentation의 정확도를 떨어뜨리게 됩니다. 본 논문에서는 방금 언급한 모호함에 더 robust한 segmenter(segmentation하는 model)를 만들고 진짜같이 다양한 examples들을 model에 학습함으로서 해결하게 됩니다. 또한 single-atlas를 가지는 경우만 고려하여 atlas-based segmentation 성능보다 더 높은 성능을 내는 것을 증명합니다. 만약 single-atlas가 아니더라도 이를 활용할 수 있습니다.
Supervised learning은 biomedical segmentation이 최근 몇 년간 인기를 가지고 있던 방법입니다. 이전에 언급했다싶이 supervised learning은 충분한 양의 data와 그에 대응되는 label에 의존성이 높다고 하였습니다. 이 의존성을 완화시키기 위해서 hand-engineered preprocessing을 활용하게 됩니다.
Semi-supervised learning과 unsupervised learning 역시 적은 dataset의 문제에 대항하여 사용되어 왔습니다. 이 방법들은 image와 그에 대응되는 segmentation data를 필요로 하지 않습니다. 이들은 segmentation의 모음을 활용해서 해부학적 우선순위를 만들어내고 adversarial network를 학습하고나 novel semantic constraint를 학습하게 됩니다. 실제로 image의 모음들은 segmentation보다 더 쉽게 사용된다고 합니다. 본 논문에서는 unlabeled image의 set들을 활용하게 됩니다.
2.2. Spatial and appearance transform models
Image의 shape와 appearance를 위한 model은 image 분석에 있어서 다양하게 활용되었습니다. medical image registration에서 spatial deformation model은 image들간 sementic corresponding(의미있는 일치)를 활용하게 됩니다. 이 분야는 optimization-based 기법과 learning-based 기법 모두 사용됩니다. 본 논문에서는 최근에 unsupervised learning-based 기법을 사용한 VoxelMorph을 spatial transformation을 학습하기 위해서 활용되었습니다.
medical image registration 기법들은 주로 intensity-normalized image나 intensity에 의존하는 objective function에 초점을 맞추어 발전하였습니다. 하지만 이러한 방법들은 image intensity의 변화를 명시적으로 알려주지 않았습니다. unnormalized image에 대해서 intensity transform model은 MRI로부터 intensity bias 효과를 제거하기 위해서 사용되어왔습니다. Spatial transformation model과 appearance transformation model은 texture과 shape이 다른 image들의 registration하기 위해 사용되어 왔습니다. 많은 연구들은 image의 shape과 texture을 만들어내는 통계적 model인 Morphable Models나 Active Appearance Models(AAM) framework로 만들어졌습니다. AAM은 해부학적인 landmark를 잡은 뒤 segmentation을 수행합니다. 본 논문에서는 unconstrained spatial transformation model과 intensity transformation model을 학습하기 위해서 AAM에서 사용된 개념을 바탕으로 CNN을 적용하여 구현하였습니다. registration이나 segmentation를 최종 목표로 삼고 transformation model을 학습하는 대신 새로운 examples를 합성하기 위해서 이러한 tranformation models로부터 sampling하게 됩니다. 이후 실험 단계에서 나오듯이 augmentation을 한 뒤의 segmentation이 transformation model을 직접 사용해서 segmentation을 수행한 것보다 더 robust함을 증명할 수 있습니다.
2.3. Few-shot segmentation of natural images
Few-shot segmentation은 semantic segmentation과 video object segmentation에서 굉장히 어려운 task입니다. 현재 존재하는 접근 방식은 대부분 natural image, 즉 풍경 사진과 같이 일상적인 image에 초점이 맞추어져 있습니다. Few-shot sementic segmentation 기법은 segment할 class의 prototype으로부터 정보를 얻어야합니다. Few-shot video segmentation은 각각의 frame의 object들이 label된 참조 frame에 배정됨으로서 자주 구현됩니다. 하지만 medical image의 경우 natural image와는 다른 어려운 점이 존재합니다. 예를 들어 tissue class간 시각적 차이는 자세히 봐야합니다. 이전에 언급했듯이 단순히 image간 intensity의 차이일 수도 있지만 실제로 tissue의 class 다를수도 있기 때문이죠.
2.4. Data augmentation
Image-based supervised learning task에서 data augmentation은 rotation과 scaling과 같은 간단한 parameterized transformation을 사용하여 구현할 수 있습니다. 이러한 parameterized transformation은 overfitting을 감소시키고 test performance를 향상시킵니다. 하지만, 이러한 성능 향상은 transformation의 종류가 parameter에 크게 의존하기 때문에 시간이 없거나 computing power가 충분하지 않다면 최적의 transformation 종류와 parameter를 탐색할 수 없을 것입니다.
최근 연구는 data로부터 data augmentation transformation을 학습하는 것을 제시하고 있습니다. 본 논문에서는 appearance transformation model과 spatial transformation model을 학습하고 MRI segmentation에 집중하였습니다. 다른 접근 방식으로 간단한 transformation 함수의 조합을 학습하는 데 초점을 두기도 합니다. 또한, deep learning network를 통해 성능을 최고로 올리는 augmentation 정책을 찾기도 합니다. 하지만 이러한 간단한 transformation의 경우 MRI image 사이의 미묘한 transformation을 capture하기에 충분치 않습니다.
3. Method
다시 돌아가서 본 논문에서 제안하고자 하는 것은 semi-supervised learning 기반으로 새로운 data를 생성해서 one-shot biomedical image segmentation임을 상기하겠습니다. 먼저, 몇 가지 기호에 대해서 정의를 하고 진행하겠습니다.
1). brain MRI biomedical image가 있을 텐데, 한 환자별로 image가 1개만 있는 것이 아니라 slice되어 전부 모으게 되면 3차원 image가 만들어지게 될 것입니다. 이 3차원 image를 $y^{(i)}$라고 하며 논문에서는 volume으로 표현합니다..
2). $x$는 atlas image이고 $l_{x}$는 $x$에 대응되는 label이 있는 참조 volume입니다. 쉽게 말해서 $l_{x}$는 segmentation map으로 볼 수 있겠습니다. 2개를 하나로 묶어서 $(x, l_{x})$로 표현합니다.
1)에서 언급했다싶이 MRI이미지 이기때문에 $x$와 $y$는 모두 3D volume입니다.
그리고 data augmentation을 구현위해서 2개의 단계를 거치게 됩니다.
먼저, spatial tranform model과 appearance transform model를 각각 학습합니다. 이때 spatial transform model은 label이 되있는 atlas volume와 label이 없는 volume 사이의 해부학적 차이를 capture하고 appearance transform model은 label이 되있는 atlas volume와 label이 없는 volume 사이의 appearance의 차이를 capture하게 됩니다. 이때 appearance란 intensity로 동일한 의미로 사용할 수 있습니다.
그리고 학습된 transform model들을 이용해서 label이 있는 volume을 합성하게 됩니다. 먼저 spatial transform model와 appearance transform model을 사용해서 atlas volume에 적용한 뒤 얻는 $\hat{y}^{(k)}$와 spatial transform model만 적용해서 얻는 $\hat{l}^{(k)}_{y}$을 통해 새로운 label이 있는 dataset으로 $(\hat{y}^{(k)}, \hat{l}^{(k)}_{y})$을 얻게 됩니다.
이때 unlabeled dataset으로부터 spatial, appearance trasform만 적용하여 새롭게 dataset을 얻었으므로 이 새로운 dataset에는 unlabeled dataset에 들어가 있는 해부학적 특성과 외형적 특성을 지니고 있을 것입니다.
3.1. Spatial and appearance transform models
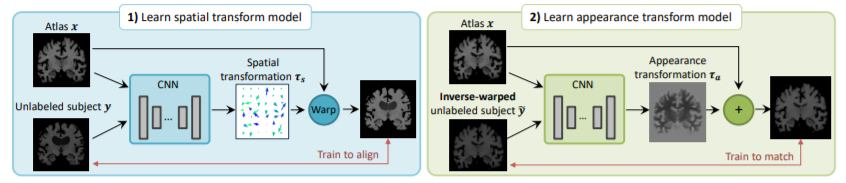
이번 절에서는 data augmentation을 위한 첫번째 단계인 spatial transform model과 appearance transform model을 학습하는 과정을 설명하고 있습니다. 이때 transform을 $\tau(\cdot)$으로 표기하게 됩니다. 물론 이 transform은 spatial transform인 $\tau_{s}(\cdot)$과 appearance transform인 $\tau_{a}(\cdot)$의 composition으로 정의됩니다. 즉 $\tau(\cdot)=\tau_{s}(\tau_{a}(\cdot))$입니다.
이때 spatial transformation은 voxel 별로 displacement field $u$의 형태로 얻어지게 됩니다. 간단하게 vector field의 형태로 나온다고 보면 될 것 같습니다. 그럼 $\tau_{s}(\cdot)$은 atlas $x$와 unlabeled $y$사이의 spatial difference가 나오게 됩니다. 즉, atlas $x$를 적당한 registration을 통해서 unlabeled dataset에 있는 해부학적 특성에 맞도록 바꿔주는 역할을 하게 되는 것이죠.
본 논문에서는 위 과정을 더 자세하게 설명하고 있습니다. 먼저 deformation function $\phi = id + u$을 정의합니다. 이때 $id$는 identical function이고 $u$는 방금 언급한 displacement field입니다. $x \circ \phi$를 atlas $x$에 deformation $\phi$을 적용한 결과라고 표기하겠습니다. dataset에서 spatial transformation의 분포를 modeling을 하기 위해서 atlas $x$를 각각의 $y^{(i)}$에 $\phi^{(i)}=g_{\theta_{s}}(x, y^{(i)})$ deformation을 계산해야합니다. 이때 $g_{\theta_{s}}$는 CNN으로 구현합니다. appearnce tranformation을 위해서 $y^{(i)}$에서 $x$로 mapping하는 inverse deformation을 $(\phi^{-1})^{(i)}=g_{\theta_{s}}(y^{(i)}, x)$로 얻을 수 있습니다. 물론 이것은 정확한 inverse는 아닙니다. 본 논문에서는 inverse로 approximation한다고 언급하였습니다.
그 다음으로 appearance transformation $\tau_{a}(\cdot)$을 atlas image의 spatial frame에 voxel 별 덧셈을 통해서 얻게 됩니다. 이때 voxel 별 volume을 얻기 위해서 함수 $\psi^{(i)}=h_{\theta_{s}}(x, y^{(i)} \circle (\phi^{-1})^{(i)})$를 사용합니다. 여기서 $y^{(i)} \circle (\phi^{-1})^{(i)}$은 이전에 학습한 spatial model를 사용해서 atlas 공간으로 $y^{(i)}$를 registration을 한 것입니다. 또한 여기서 $h_{\theta_{a}}$도 CNN으로 구현하게 됩니다.
3.2. Learning
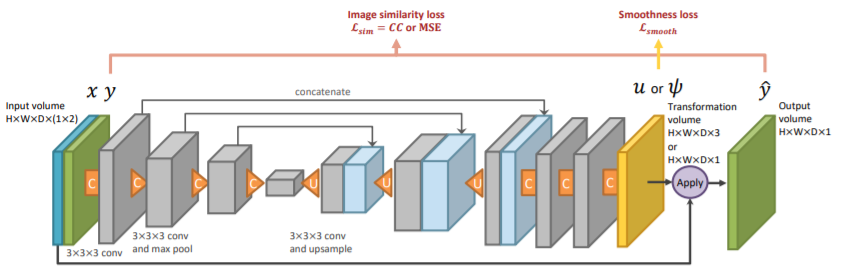
이전 절에서 설명했듯이 atlas volume과 unlabeled volume 사이의 transform $\tau_{s}(\cdot)$와 $\tau_{a}(\cdot)$ transform의 분포를 capture하는 것이 목표입니다. 이는 위의 그림의 CNN 구조를 사용합니다. 구조 자체는 U-net 구조와 상당히 유사하며 다른 점은 input이 atlas $x$, unlabeled $y$가 함께 들어가고 Convolution layer를 3번 더 추가하여 얻은 transformation을 을 altas $x$에 적용하여 새로운 data인 $\hat{y}$를 얻게 됨니다. 이때 spatial transformation이라면 위 구조는 $g_{\theta_{s}}$가 되고 appearance transform이라면 위 구조는 $h_{\theta_{a}}$가 됩니다. 구조 자체는 $g$와 $h$가 동일하지만 다른 함수 이름을 쓴 것은 얻는 transformation과 연산의 차이 때문입니다. $g$의 경우 registration을 위한 spatial transformation을 얻고 거기에 atlas $x$에 warp하게 됩니다. 하지만 $h$의 경우 unlabeled에 분포된 intensity로 바꾸기 위한 appearance transformation을 얻고 거기에 atlas $x$에 voxel별 합을 적용하게 됩니다.
본 논문에서 추가적으로 설명하고자 하는 것은 spatial model인 $g_{\theta_{s}}$입니다. 본 논문에서는 VoxelMorph의 학습 방식을 활용했다고 언급하였습니다. VoxelMorph의 경우 displacement field smoothness term과 image similarity loss를 결합적으로 최적화함으로써 image가 다른 image에 register하는 smooth displacement vector field를 output으로 얻어 학습한다고 하였습니다. 본 논문에서는 image similarity loss로서 normalized cross-correlation으로 VoxelMorph를 사용하는 것 대신에 $g_{\theta_{s}}$가 unnormalized input volume에도 추정가능하도록 사용하였습니다.
appearance model 역시 비슷한 방식으로 학습을 하게 됩니다. 이전 절에서 정의한 $h_{\theta_{a}}$를 단순하게 atlas space에서의 voxel 별 뺄셈으로 정의할 수도 있습니다. 물론 이러한 transformation은 target image를 완벽하게 얻을 수 있겠지만 registeration function(deformation function)인 $\phi^{-1}$이 완벽하지 않다면 큰 왜곡을 불러올 수도 있습니다. 이로인해서 해부학적 label와 일치하지 않는 $x + \psi$ image가 생성될 것입니다. 대신에 $h_{\theta_{a}}$를 해부학적 불변성을 바탕으로 voxel 별 intensity 변화율을 생성하는 신경망을 설계합니다. 이제 신경망 output이 $\psi^{(i)}=h_{\theta_{a}}(x, y^{(i)} \circle \phi^{i})$로 주어졌을 때 atlas segmentation map에 기반하는 smoothness regularization function을 정의합니다.
$$L_{smooth}(c_{x}, \psi)=(1-c_{x}) \nabla \psi$$
$c_{x}$는 atlas segmentation label인 $l_{x}$로부터 계산된 해부학적 경계의 binary image입니다. 그리고 $\nabla$는 spatial gradient operator입니다. 이 식을 해석해보겠습니다. $c_{x}$가 $x$에 대한 segmentation label이기 때문에 $1-c_{x}$는 $x$에 대한 segmentation label이 아닙니다. 그리고 $\nabla \psi$은 appearance transformation의 gradient입니다. 직관적으로 생각해보면 서로 다른 label일 때 $\nabla \psi$는 커질 것입니다. 하지만 서로 같은 label일 때는 $\nabla \psi$가 극단적으로 커지지는 않을 것입니다.
이제 appearance model의 모든 loss $L_{a}$를 확인하겠습니다. 본 논문에서는 image similariry loss로 mse를 주었습니다. 따라서 $L_{sim}(\hat{y}, y)=\left|| \hat{y} - y \right||^{2}$입니다. 여기에 방금 언급한 smoothness regularization function을 더해서 appearance model의 $L_{a}$를 정의합니다.
$$L_{a}(x, y^{(i)}, \phi^{(i)}, (\phi^{-1})^{(i)}, \psi^{(i)}, c_{x})=L_{sim}((x+\psi^{(i)}) \circle \phi^{(i)}, y^{i}) + \gamma_{a}L_{smooth}(c_{x}, \psi^{i})$$
이때 $\gamma_{a}$는 hyperparameter입니다.
3.3. Synthesizing new examples
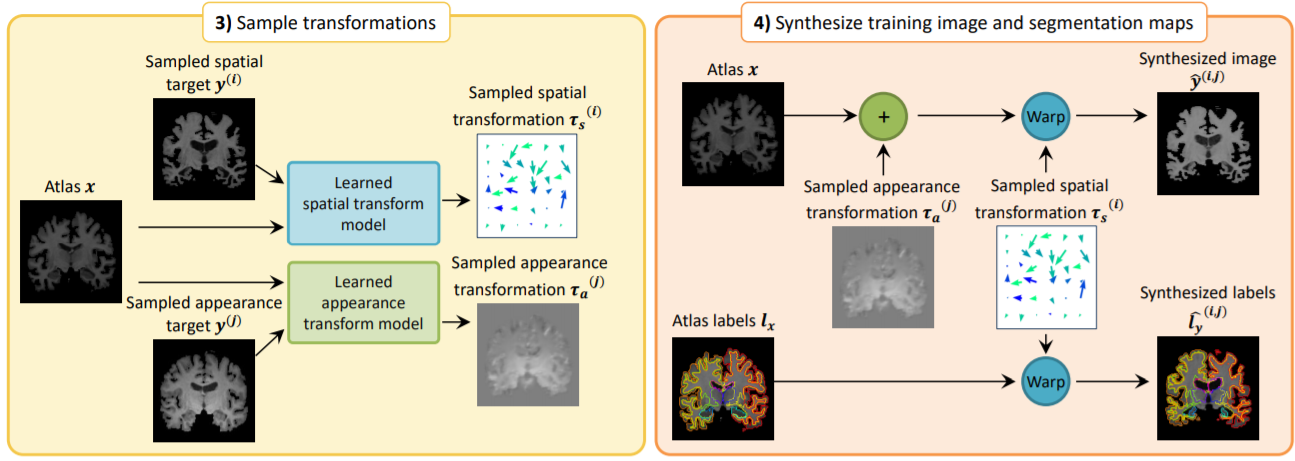
이전 절에서 언급한 model들을 통해서 unlabeled dataset으로 부터 target volume인 $y^{(i)}$, $y^{(j)}$를 한 개씩 sampling하여 spatial transformation $\tau_{s}^{(i)}$와 appearance transformation $\tau_{a}^{j}$를 sample(여기서 'sample'을 사용한 것은 각기 다른 target volume을 1개씩 sample했기 때문입니다.)할 수 있게 합니다(왼쪽 그림). 이때 sampling된 spatial target과 appearance target이 서로 다른 대상일 수도 있기 때문에 본 논문에서는 한 대상의 spatial transformation과 다른 대상의 appearanve transformation 조합하여 새로운 single synthetic volume $\hat{y}^{(i, j)}$를 생성하여 사용할 수 있는 방법을 제시하였습니다(오른쪽 그림). 새롭게 생성된 $\hat{y}^{(i, j)}$에 대응되는 새로운 label $\hat{l}^{(i, j)}_{y}$는 어차피 binary image이기 때문에 appearance transformation은 고려할 필요없고 동일한 spatial transformation만 적용하여 얻을 수 있습니다. 이를 식으로 쓰면 $\hat{y}^{(i, j)}=\tau_{s}^{i}(\tau_{a}^{j}(x))$, $\hat{l}^{(i, j)}_{y}=\tau_{s}^{i}(l_{x})$가 됩니다. 위 그림에서 그 과정이 나타나 있습니다. 이렇게 얻은 새로운 dataset은 이후의 segmentation training dataset에 추가되어 학습에 쓰입니다.
3.4. Segmentation network
이전 절에서 얻은 새로운 dataset을 통해 supervised-based segmentation network의 성능이 향상되는 지 확인합니다. 이떄 사용되는 network는 SOTA 성능을 내는 network로 사용할 예정입니다. 어떤 network인지는 experiment 부분에서 설명하도록 하겠습니다. 이때 본 논문에서는 연구실의 GPU 성능 문제로 인해서 새로 증강된 training data를 random으로 조금씩 나눠서 훈련을 진행합니다. epoch 수는 validation set을 기준으로 early stopping을 이용해서 정했습니다.
3.5. Implementation
본 논문의 상세 코드는 keras와 tensorflow 기반으로 작성하였습니다. image에 spatial transformation의 적용은 differentiable 3D spatial transformer layer를 통해 구현되었습니다. 간결하게 하기 위해서, forward를 capture하고 3.1.절에 설명한 inverse spatial transformation을 2개의 identical 신경망을 통해 구현하였습니다. appearance transform model을 구현하기 위해 $L_{a}$의 hyperparameter인 $\gamma_{a}$를 0.02로 고정하였습니다. 본 논문에서 transform model을 학습하기 위해서 각 epoch마다 volume의 single pair를 사용했고 segmentation model을 학습하기 위해서 batch size를 16으로 나누었습니다. 모든 model들은 learning rate가 $5e^{-4}$로 사용되었습니다.
4. Experiment
본 논문에서는 brain MRI segmentation 성능의 향상을 목표로 automatic augmentation을 하고자 한다. 특히, segmentation시 unnormalized data에 대해서 수행하여 실제 데이터에 대해서도 robust함을 보이고자 한다.
4.1. Data
본 논문에서 사용한 dataset은 총 8가지이다.(ADNI, OASIS, ABIDE, ADHD200, MCIC, PPMI, HABS, Harvard GSP) 그리고 segmentation label은 FreeSurfer를 통해서 계산하였다. 전처리 과정은 전체 뇌가 있으면 그 뇌를 1mm 단위로 잘라서 256 $\times$ 256 $\times$ 256으로 만듭니다. 이제 적절하게 image를 적절하게 자르고 정렬해서 160 $\times$ 192 $\times$ 224로 만듭니다. 이때 intensity를 전부 맞추는 과정은 하지 않습니다.
4.2. Segmentation baselines
1) Single-atlas segmentation(SAS)
비교하는 대상으로 SOTA 성능을 가지는 image registration 모델을 선택합니다. 선택한 image registration model을 바탕으로 각각의 test volume에 atlas를 regiser합니다. 그리고 deformation field를 사용해서 atlas label에 적용합니다. 즉, 각각의 test image $y^{(i)}$에 대해서 $\phi^{(i)}=g_{\theta_{s}}(x, y^{(i)})$를 얻습니다. 이전에 설명한 $\phi$는 $x$가 $y^{(i)}$의 spatial deformation을 적용해서 register 시킵니다. 그리고 label $\hat{l}_{y}^{(i)}=l_{x} \circle \phi^{(i)}$를 predict합니다.
2). Data augmentation using single-atlas segmentation(SAS-aug)
위의 SAS 결과 중 label을 unannotated training dataset에 대한 label로 사용하게 됩니다. 그리고 하나의 segmentation dataset을 구성하게 되면 이 dataset은 supervised segmentation을 위한 training example로 사용됩니다. 이 경우 100개의 training example을 추가하였습니다.
3). Hand-tuned random data augmentation(rand-aug)
sparse grid에서 random vector를 sampling하고 bilinear interpolation과 spatial blurring을 적용함으로서 새로운 random smooth deformation field를 생성합니다. 또한 $[0.5, 1.5]$의 범위에서 uniform하게 sampling된 global intensity multiplicative factor를 사용해서 다른 intensity 값을 가지는 image를 합성합니다. 2가지 방법 중에 매 학습마다 random하게 변형된 새로운 image를 합성하게 됩니다.
4). Supervised
계속 말해왔듯이 training dataset의 모든 101개의 example들에 대한 ground truth label을 사용하는 fully-supervised segmentation network를 사용합니다.
4.3. Variants of our method
1). Independent sampling(ours-indep)
새로운 dataset을 합성하는 과정을 설명한 3.3 절에서 언급했듯이 독립적으로 sample spatial target images($\tau_{s}^{(i)}$)와 sample appearance target images($\tau_{a}^{(j)}$)를 얻게 됩니다. unlabeled 100개의 target image에 대해서 독립적으로 $\tau_{s}^{(i)}$와 $\tau_{a}^{(j)}$를 sample하므로 총 10,000개의 각기 다른 labeled example을 얻을 수 있습니다. 하지만 메모리의 한계로 training set에 10,000개의 새로운 dataset을 추가하는 것 보다는 매 training 마다 random labeled example을 합성하는 것을 선택합니다.
2). Coupled sampling(ours-coupled)
3.3 절에서 제시한 transformation model를 독립적으로 적용하는 것의 효율성을 증명하고자 ours-indep 독립적으로 transformation model을 얻는 것이 아니라 같은 image에서 얻는 결과를 비교하게 됩니다. 현재 unlabeled 100개의 dataset이 존재하기때문에 최대 100개의 dataset을 얻을 수 있습니다. ours-indep와 같이 training dataset에 추가하는 것이 아니라 매 training 마다 random labeled example을 합성하는 것을 선택하였습니다.
3). Ours-indep + rand-aug
뿐만 아니라 rand-aug에 ours-indep를 함께 적용하여 매 training마다 새롭게 합성된 example을 model에게 제시하게 됩니다. 이를 통해서 한번도 보지못한 unlabeled image에 대해서도 segmenter의 robustness를 향상시켰음을 보여주고 있습니다.
4.4. Evaluation metrics
본 논문에서는 해부학적 영역 사이의 중첩의 정도를 측정하는 Dice score를 통해서 성능을 측정합니다. 이때 Dice score 1은 두 영역이 완전히 겹치는 것을 의미하고 Dice score 0은 두 영역 하나도 겹치지 않는 것을 의미합니다. 따라서 Dice score는 1에 가까울수록 좋은 segmentation 성능 가진다고 볼 수 있습니다.
4.5. Results
4.5.1 Segmentation performance
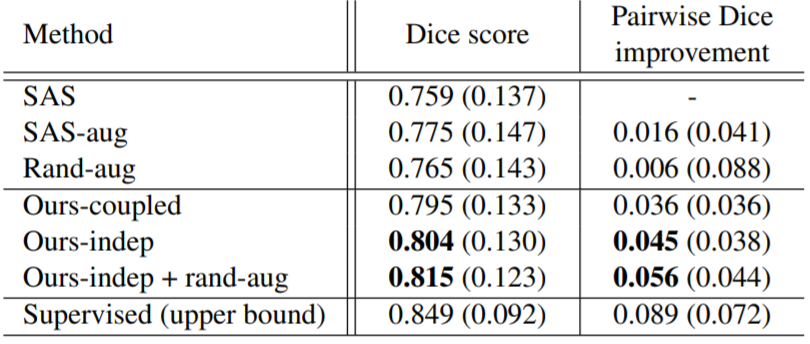
이 표는 이전 절에 제시한 방법에 대한 각각의 segmentation accuracy를 보여주고 있습니다. 본 논문의 방법은 30개의 해부학적 label에 대해서 모든 baseline 방법보다 더 좋은 mean Dice score를 내고 있습니다.(괄호의 숫자는 표준 편차입니다.)
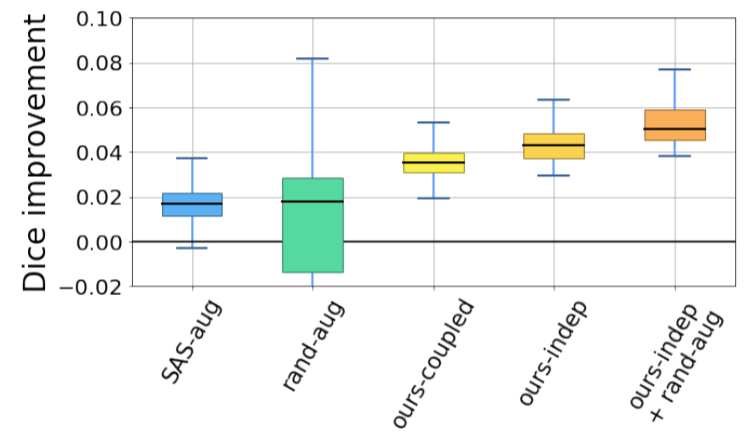
이 그림은 30개의 해부학적 label에 대한 SAS 방법과 비교해서 얼마나 향상되었는 지를 mean Dice score를 기준으로 나타낸것입니다. 하지만 rand-aug의 성능이 가장 높을 때가 있었습니다. 그러나 평균적으로 봤을 때 rand-aug는 본 논문에서 제안하는 방법에 비해서 일관적이지 않다라고 볼 수 있습니다. 왜냐하면 rand-aug의 평균이 다른 기법에 비해서 낮기 때문이지요.
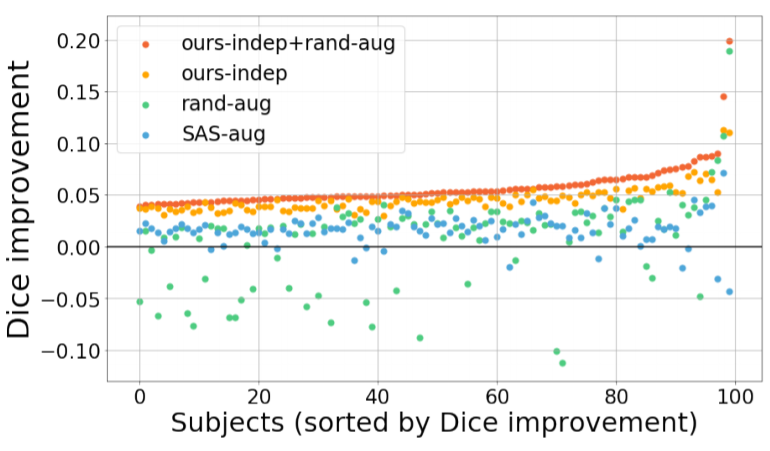
이 그림은 Ours-indep + rand-aug가 모든 test subject에 비해서 더 일관적으로 증가하고 있음을 보여주고 있습니다. 물론 rand-aug를 사용하지 않은 Ours-indep만 사용해도 모든 test subject에 대해서 SAS와 SAS-aug 결과보다 더 좋은 성능을 내고 있습니다. 또한 rand-aug와 비교했을 때도 5개만 향상 정도가 적고 남은 95개의 test subject에 대해서는 향상 정도가 더 높은 것을 볼 수 있습니다.
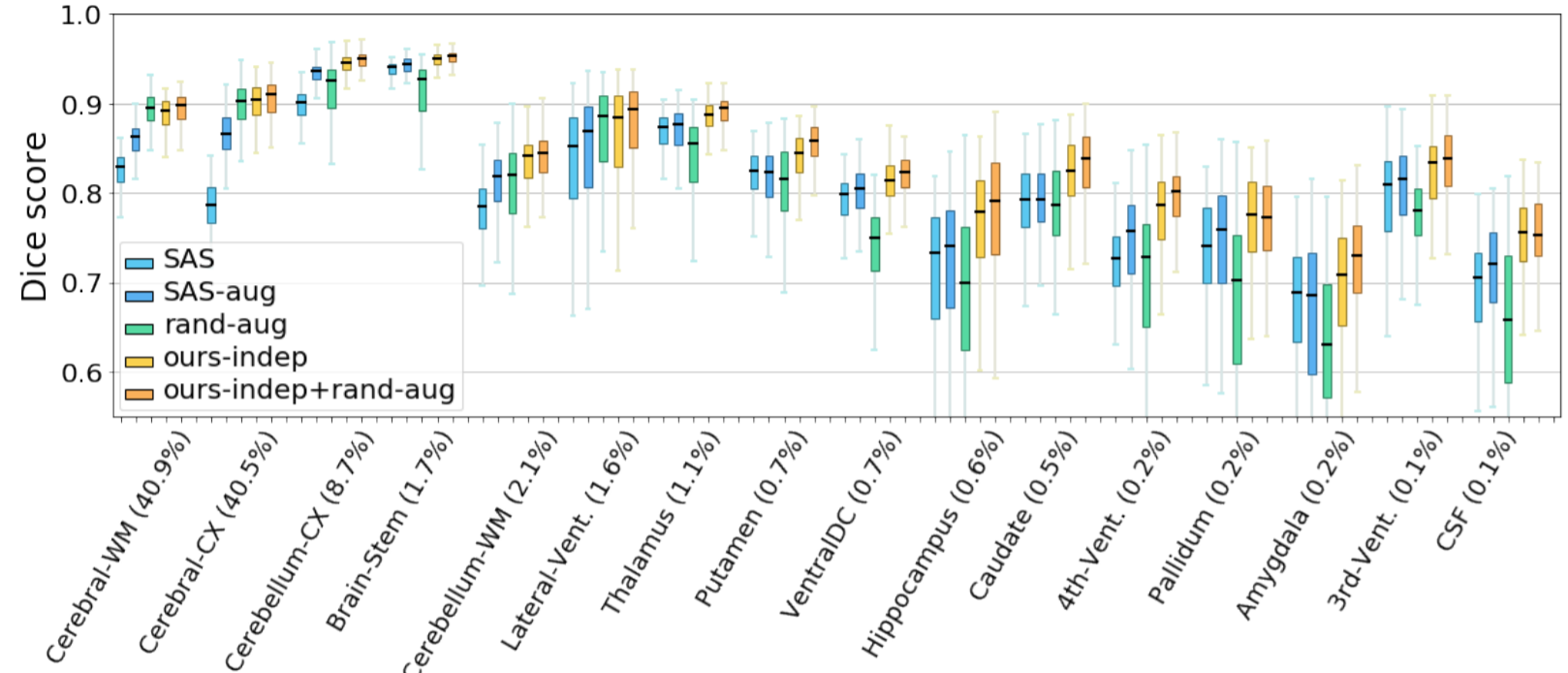
이 그림에서 $x$의 의미는 잘 모르겠지만 본 논문에서 언급하는 것으로 봤을 때 해부학적 구조의 크기인 것으로 볼 수 있습니다. rand-aug 자체는 큰 해부학적 구조에서는 SAS보다 Dice score가 더 높습니다. 하지만 오른쪽으로 갈수록 해부학적 구조의 크기가 작아지는 데 이는 rand-aug가 작은 해부학적 구조에 대해서는 좋지 않은 적용이라는 것을 보여주고 있습니다. 하지만 본 논문에서 제시하는 모든 방법은 해부학적 구조의 크기와 관계없이 다른 방법보다 Dice score가 다 높은 것을 볼 수 있습니다.
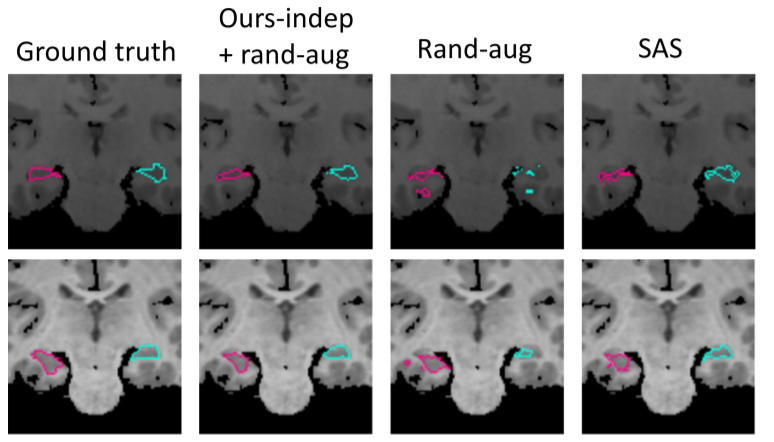
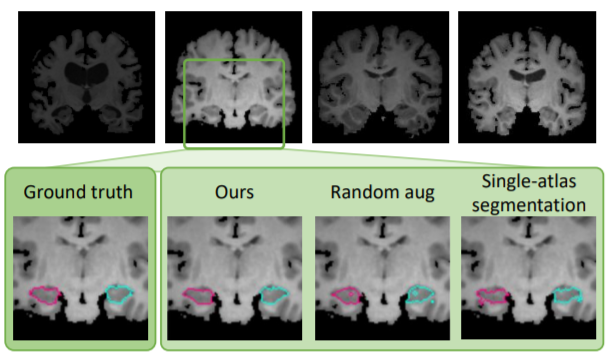
이 그림은 뇌의 해마 부분을 2개의 test subgect에 대해서 segment한 예시입니다. 맨 왼쪽이 Ground Truth인데 실제로 작은 해부학적 구조를 가지는 해마를 rand-aug는 부적합한 것을 볼 수 있습니다. 하지만 두번째 열을 보면 본 논문에서 제시한 방법과 rand-aug를 함께 사용한 결과가 휠씬 적합한 것을 볼 수 있습니다.
4.5.2 Synthesized image
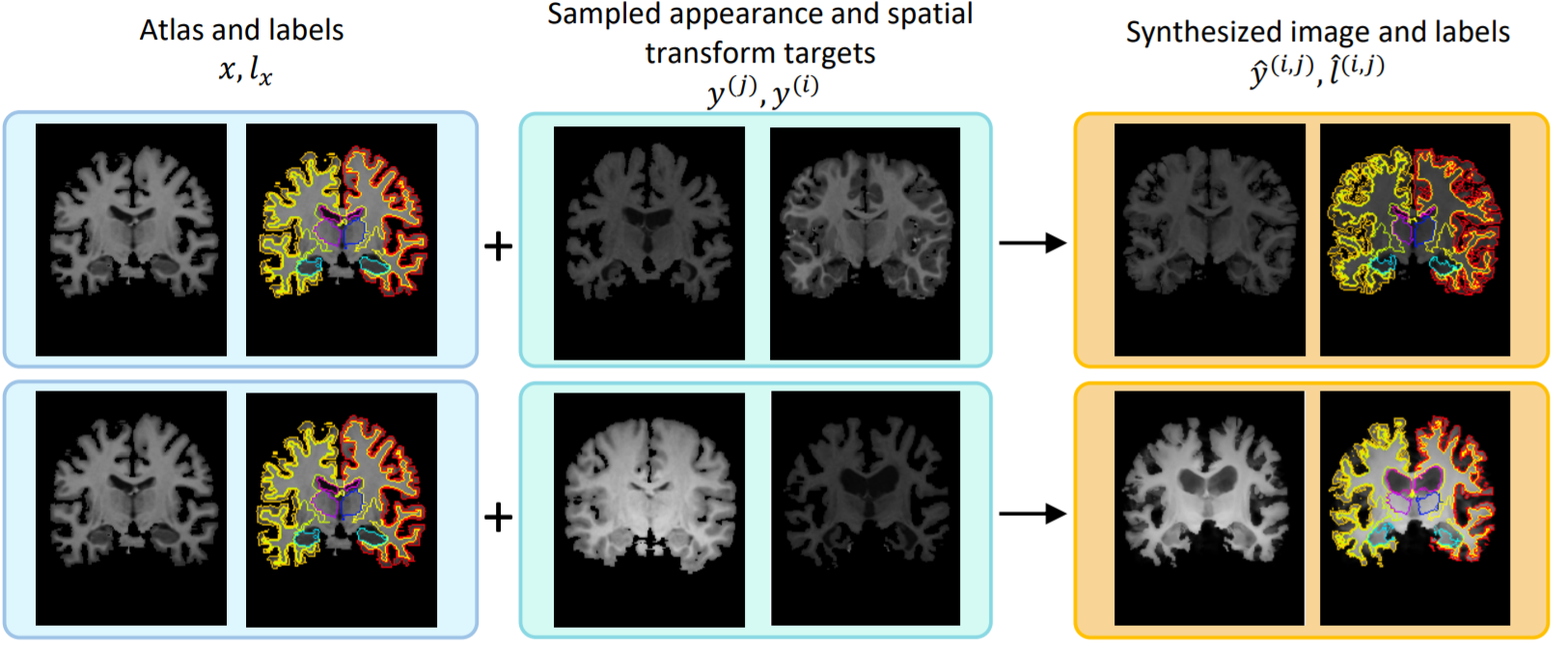
본 논문에서 제시하는 data 합성 방법은 굉장히 많은 조합의 brain appearance를 나타낸다고 언급하였습니다. 이 그림은 unlabeled image를 합성한 그 예시입니다.
현재 다양한 방법으로 논문을 리뷰해보려고 했는데 이번에는 통째로 해석과 제가 이해한 바탕으로 작성해보았습니다. 음... 아무래도 이 방법도 너무 시간이 오래걸려서 다른 블로거들의 논문 리뷰를 더 많이 읽어봐야겠습니다.
