안녕하세요. 오랜만에 논문 리뷰 포스팅을 하게 되었습니다. 이전에도 논문은 간간히 읽었는 데 포스팅 해야된다는 것을 까먹고 이제 올리게 되었습니다. 오늘 리뷰할 논문은 사실 이전에 제가 올렸던 segmentation, data augmentation과는 다른 주제를 가지고 있습니다. 이 논문은 Frequency domain이 CNN의 일반화 성능을 어떤 식으로 도와줄 수 있는 지에 대해서 설명하고 있는 논문입니다. 바로 시작해보도록 하죠.
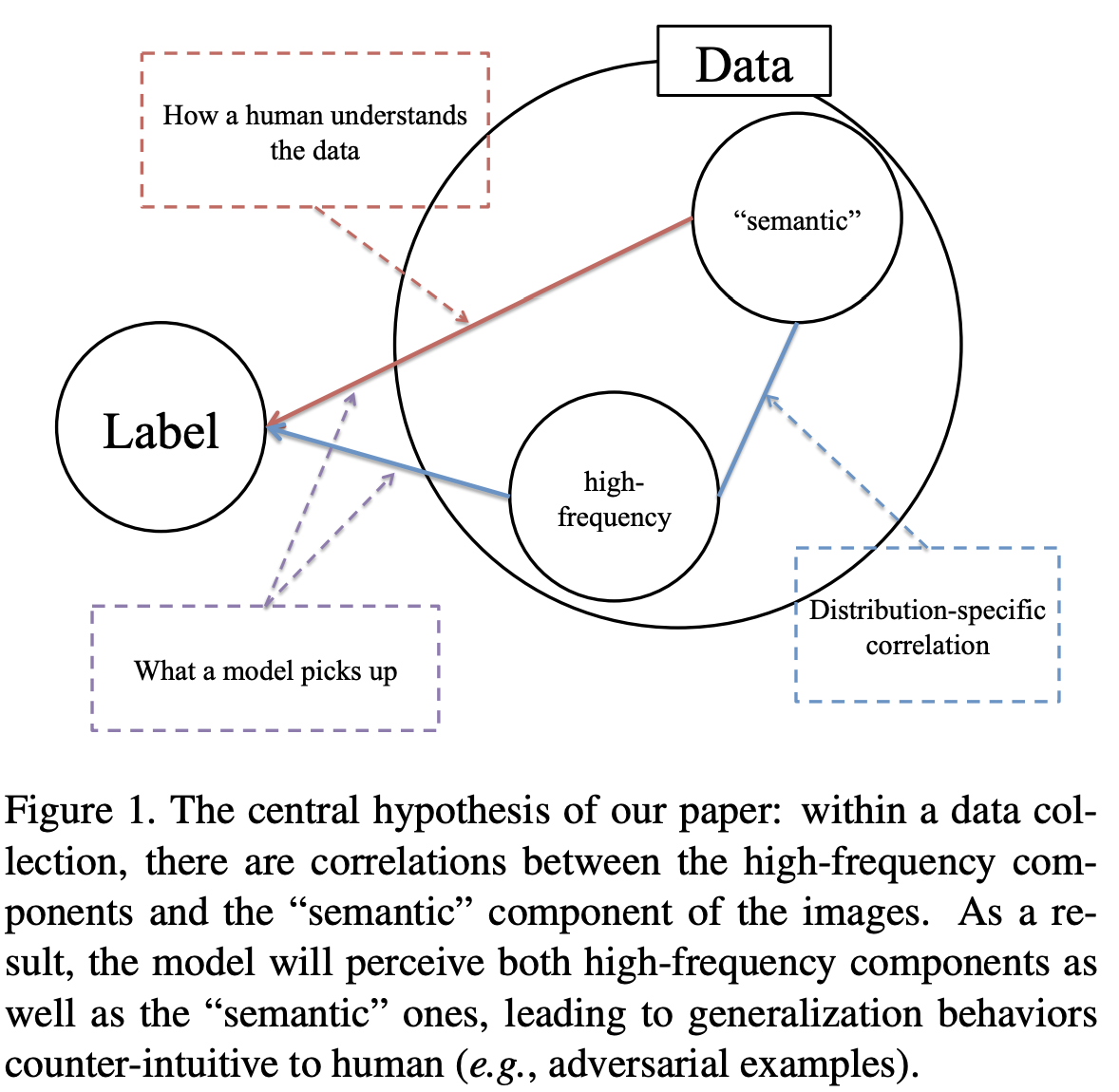
이 논문의 중심 가정은 frequency domain의 high component와 image semantic 간의 어떤 관계가 있다는 것입니다. Figure 1은 설명하면 high frequency와 image semantic 간에는 분명히 분포를 통해서 관계성이 존재할 것입니다. 왜냐하면 결국에는 하나의 이미지로부터 얻는 것이기 때문이죠. 하지만 사람의 이미지 인지 과정에는 high frequency는 관여하기 힘듭니다. 일단 high frequency 영역을 따로 분리한 뒤 spatial domain에서 다시 그려보면 사람이 봤을 때 알아보기 힘들기 때문이죠. 따라서 사람은 이미지가 주어졌을 때 image semantic 만을 보고 판단한다고 가정하는 것을 큰 무리가 없을 것입니다. 사람은 그렇지만 저희가 구현한 딥 러닝 모델은 어떨까요?

위 그림을 통해서 방금 전의 질문에 답을 할 수 있습니다. 각 그림에서 첫번째 열은 high frequency component, low frequency component가 같이 있는 이미지, 두번째 열은 low frequency만 추출한 이미지, 세번째 열은 high frequency만 추출한 이미지입니다. 처음에 제가 언급했듯이 high frequency를 spatial domain으로 이미지화하면 사람이 봤을 때는 알아보기 힘듭니다. 각 열에 대한 아래의 막대 그래프는 해당 데이터를 학습된 모델을 이용해서 확률 기반으로 예측한 것입니다. 사람의 관점에서 봤을 때는 분명 첫번째 열과 두번째 열의 이미지가 쉽게 알아볼 수 있을 거 같지만, 오히려 세번째 열에 대한 예측이 더 정확한 것을 볼 수 있습니다. 이 결과를 통해 알 수 있는 것은 CNN 모델은 low frequency 뿐만 아니라 high frequency 역시 예측에 중요하게 작용한다는 것입니다. 이 것은 통념적인 저희의 예상과는 크게 다른 결과입니다. 이를 기반으로 이 논문에서는 다양한 질문을 던집니다.
1. High-frequency Components & CNN's Generalization
1.1. CNN Exploit High-frequency Component
먼저, high frequency component가 CNN의 일반화 성능에 어떤 영향을 끼치는 지 분석을 해보도록 하겠습니다. 이때, HFC는 High-frequency Component, LFC는 Low-frequency Component로 줄이도록 하겠습니다. 주어진 이미지 $x = \{x_{l}, x_{h}\}$로 항상 분리할 수 있습니다. $x_{l}$는 이미지의 LFC, $x_{h}$는 이미지의 HFC입니다. 그러면 아래의 4개의 수식을 만족하게 됩니다.
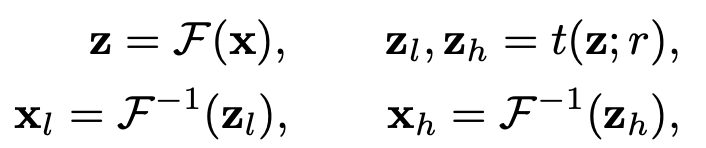
여기서 각각 $F, F^{-1}$는 푸리에 변환, 역푸리에 변환 입니다. $z$는 이미지 $x$의 frequency domain입니다. $t(\dot;r)$는 반지름이 $r$인 ideal mask입니다. 이 기호는 LFC를 추출하게 됩니다. $r$에 따라서 얼마나 LFC의 영역이 보존될 것입니다. 그러고 통과되지 않는 나머지는 HFC입니다. 따라서, $z_{l}, z_{h}$는 각각 $x_{l}, x_{h}$에 역푸리에 변환을 적용한 것입니다. $z_{l}, z_{h}$를 좀 더 명확하게 아래와 같이 정의할 수 있습니다.
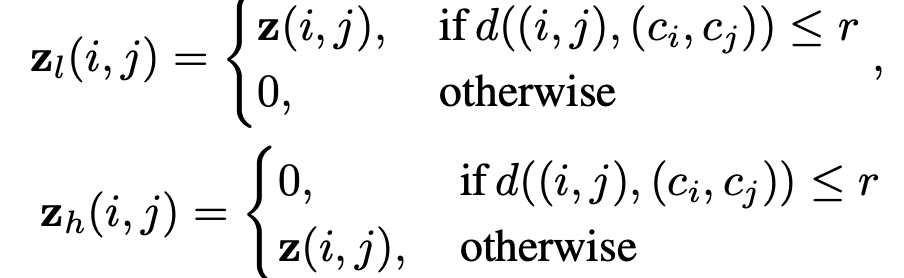
$c_{i}, c_{j}$는 $z$의 중심 좌표이고 $d(\dot, \dot)$은 거리 함수(metric function)로 여기에서는 유클리디안 거리로 정의됩니다.
Remark 1(A1). 오직 $x_{l}$만 사람에게 쉽게 인지되지만 CNN는 $x_{h}, x_{l}$ 모두 인지한다.
위 명제를 수식적으로 써보겠습니다. 먼저 "오직 $x_{l}$만 사람에게 쉽게 인지된다."부터 정리해보면 아래와 같습니다.
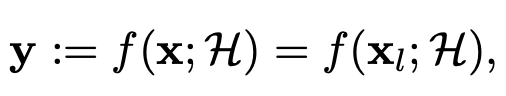
CNN은 훈련 시 아래의 수식을 사용하게 됩니다. 간단하게 해석하면 파라미터 $\theta$를 가지는 모델이 이미지 $x$를 이용해서 예측한 결과와 Ground truth 사이의 손실의 최소화하는 파라미터 $\theta$를 찾겠다는 것이죠.
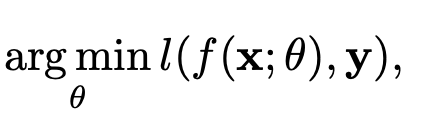
이때, 저희가 처음에 이미지는 LFC, HFC로 분리할 수 있다고 했으므로 최종적으로는 아래의 수식을 얻을 수 있습니다.
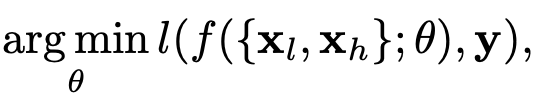
위의 수식이 의미하는 바는 CNN은 HFC를 가지고 학습을 할 수 있다는 것입니다. 이 과정을 정리하면 CNN은 사람에게 비직관적인 HFC를 학습에 사용하는 데 이 과정으로 인해서 CNN의 일반성이 사람이 봤을 때 비직관적이라는 것입니다. 즉, 분석하기 어려운 이유가 된다는 것이죠.
여기서 한 가지 주의해야할 점은 "CNN은 HFC를 가지고 학습을 할 수 있다."는 것은 "CNN에 과적합이 발생했다."는 것과는 전혀 다르다는 것입니다. 왜냐하면, $x_{h}$는 $x_{l}$에 비해서 sample-specific idiosyncrasy, 즉 이미지의 특질성을 더 많이 가지고 있고, 이는 학습, 검증 그리고 시험 과정에 일반화가 될 수 있도록 돕는 요소가 되기 때문입니다. 하지만, 이것은 사람에게는 비직관적이겠죠.
1.2. Trade-off between Robustness and Accuracy
다음으로는 CNN의 Robustness와 Accuracy 사이의 Trade-off 관계를 분석해보겠습니다. Robustness은 시험 성능이 훈련 성능과 유사한 것을 의미합니다. 하지만 훈련 성능과 시험 성능이 유사하면 오히려 Accuracy가 떨어지는 현상이 발생한다는 것이죠. 먼저, accuracy부터 정의하면 아래와 같습니다.
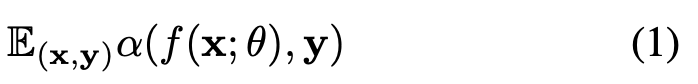
$\alpha(\dot)$은 임의의 성능 평가 지표를 의미합니다. 즉, 위 식은 모든 데이터에 대한 평균적인 성능을 의미합니다. 그리고 robustness 역시 아래와 같이 정의할 수 있습니다. 이는 이전 논문을 참고하였다고 하는군요.
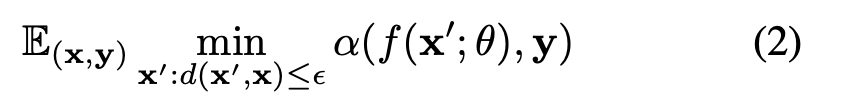
위 수식을 간단하게 설명해보죠. 어떤 데이터 $x$에 대해서 굉장히 유사한 $x'$이 존재할 것입니다. 이를 수식적으로 표현하면 $d(x, x') \le \epsilon$ 라고 적을 수 있겠죠. $x'$에 대해서 $x'$가 $y$로 예측되는 예측 정확도를 최소화시킨다는 것으로 아주 조금 다른 2개의 이미지가 주어졌을 때 $x \rightarrow y$로 예측되도록 해야지 다른 유사한 이미지인 $x' \rightarrow y$로 예측이 최대한 안된다는 것을 의미합니다.
여기서 한 가지 가정(A2)을 추가합니다. 어떤 파라미터 $\theta$를 가지는 모델에 대해서 $f(x; \theta) \neq f(x_{l}; \theta)$인 데이터가 존재한다는 것입니다. 쉽게 말하면 LFC로만 판단한 경우와 LFC, HFC를 이용해서 함께 판단하는 경우 서로 다른 결과가 나오는 데이터가 존재한다는 것이죠. 이를 통해서 아래의 따름정리를 유도할 수 있습니다.
Corollary 1. 위의 가정 A1, A2에 대해서 유클리디안 거리가 아닌 어떠한 방법으로의 거리 함수 $d(\dot, \dot)$과 $\epsilon$에 대해서 $\epsilon \ge d(x, x_{l})$인 데이터 $<x, y>$에 대해서 정확하게(accurately), 그리고 강건하게(robustly)는 예측할 수 없다.
2. Rethinking Data before Rethinking Generalization
딥 러닝 모델에 대해서 직관적으로 이해할 수 있는 것 중 하나는 모델의 capacity가 높기 때문에 충분히 데이터를 기억할 수 있다는 것입니다. 하지만 논문의 저자는 이에 대해 질문은 제기하는 데, 만약 신경망이 데이터를 쉽게 기억할 수 있다면 훈련 손실을 줄이기 위해서 바로 데이터를 기억하는 것이 아니라 어째서 데이터로부터 일반화 가능한 패턴을 배우기 위해서 노력해야할까요? 이를 실험적으로 확인하기 위해서 데이터의 label이 그대로 두고 학습해보고, 데이터의 label을 shuffle하여 실험을 해보도록 하겠습니다. 본 논문에서 주장하는 것은 데이터의 label이 그대로 있다면(이상없다면) CNN은 훈련 성능을 증가시키기 위해서 먼저 LFC를 이용하여 학습을 진행하고 다음으로 점진적으로 HFC를 선택한다고 하였습니다. 만얃 데이터의 label이 shuffle된 상태라면 LFC, HFC를 동일하게 이용하여 학습을 진행한다고 하였습니다.
실험을 위해서 사용한 데이터셋은 CIFAR10입니다. 이 말고 다른 실험에 대한 하이퍼파라미터는 논문의 본문을 참고해주시길 바랍니다. 위 문단에서 언급한 2개의 label 형태에 대해서 학습을 진행합니다. 이를 각각 $M_{\text{natrual}}, M_{\text{shuffle}}$이라고 하겠습니다. 이 실험을 통해서 확인해야하는 것은 모델이 LFC, HFC 중 어떤 정보를 먼저 선택하느냐입니다. 이를 위해서 $x_{l}$을 추출할 때 $r = 4, 8, 12, 16$으로 바꾸어 실험을 진행합니다. 여기서 중점적으로 볼 것은 $r$에 따라서 훈련 성능이 얼마나 변하는 지 입니다.
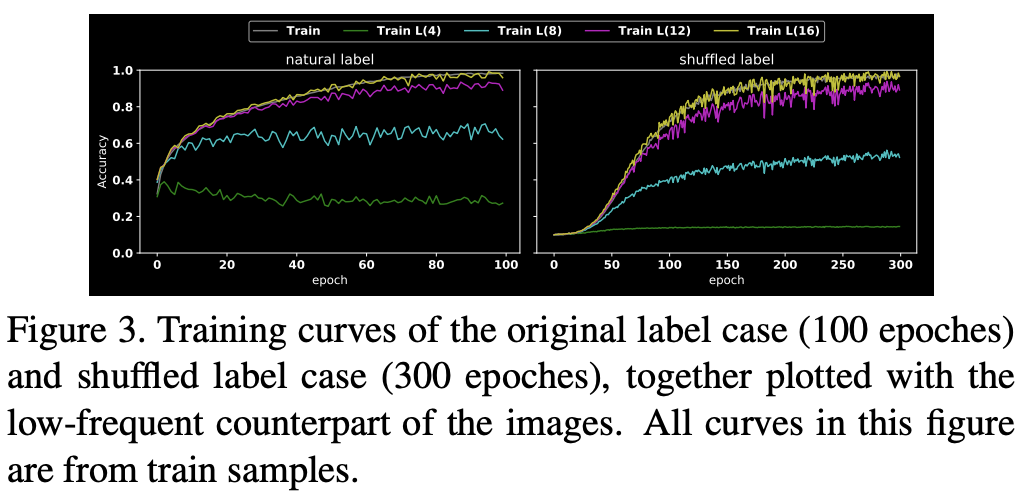
위 그림을 통해서 알 수 있는 첫번째 사실은 $M_{\text{shuffle}}$이 $M_{\text{natrual}}$에 비해서 훈련 시간이 더 오래걸린다는 것입니다. 그리고 $r = 4, 8$일 때, $M_{\text{natrual}}$의 학습 곡선을 보면 $M_{\text{shuffle}}$에 비해서 LFC를 더 많이 배운다는 것을 알 수 있습니다. 이를 확인할 수 있는 것 중 하나는 $M_{\text{natrual}}$는 $r = 4$일 때 첫번째 에폭에서 벌써 약 40%의 훈련 성능을 보이고 있습니다. $r = 4$인 것은 거의 LFC만 남았다고 볼 수 있기 때문에 이와 같은 해석이 가능합니다. 이 그래프를 통해서 $M_{\text{natrual}}$이 실제로 LFC를 더 선호한다는 것으로 해석할 수 있고, $M_{\text{shuffle}}$은 LFC, HFC 에 대한 우선순위가 없다는 것으로 해석할 수 있습니다. 사실 이 현상은 그리 놀라운 것이 아닙니다. 왜냐하면 데이터셋은 기본적으로 사람이 LFC를 보고 판단하여 직접 annotating을 한 것입니다. 그래서 당연히 훈련 성능을 증가시키려면 label에 이상이 없다는 가정 하에 CNN 모델은 LFC를 선택하는 방법이 최선일 것입니다.
3. Training Heuristic
이제부터는 모델의 일반화와 관련된 내용입니다. 모델의 일반화에는 수많은 요소가 개입되어있는 데 이에 대해서 분석해보도록 하겠습니다.

먼저, 배치 사이즈와 관련된 내용입니다. 위의 그림을 보시면 작은 배치 사이즈를 가지게 되면 훈련 성능과 시험 성능의 상승 변화가 매우 가파른 것을 볼 수 있습니다. 하지만 간격은 점점 멀어지고 있죠. 그에 반해 배치 사이즈가 커지면 훈련 성능과 시험 성능이 높지는 않지만 간격은 거의 존재하지 않습니다. 또한 일반화 간격이 HFC를 capture하는 것과 밀접한 관련이 있어보입니다. 배치 사이즈를 더 키워서 학습을 진행하면 HFC의 변화는 거의 없습니다(invariant). 이제 그만큼 일반화 간격이 거의 없다는 것을 볼 수 있습니다.

다음으로 볼 것은 일반화 성능을 증가시키기 위해서 사용되는 수많은 알고리즘들입니다. 이중에서 주목할 부분은 mix-up과 BatchNorm입니다. 두 알고리즘 모두 다른 휴리스틱에 비해서 HFC를 잘 capture하고 있습니다.
4. Adversarial Attack & Defense
만약 딥 러닝 모델의 예측이 HFC에 의존한다면 HFC의 섭동(perturbation)은 모델의 예측에 큰 변화를 줄것이라고 예상할 수 있습니다. 하지만 기본적으로 adversarial attack은 사람이 볼 수 없는 방법으로 공격을 하는 것이기 때문에 사람이 인지하는 것은 어려울 것입니다. 아래는 adversarial attack의 예시입니다. 두 이미지 모두 판다지만 노이즈를 추가하는 공격으로 인해서 다른 방향으로 예측이 됩니다. 그러나 눈으로 봤을 때는 별 차이가 없죠.
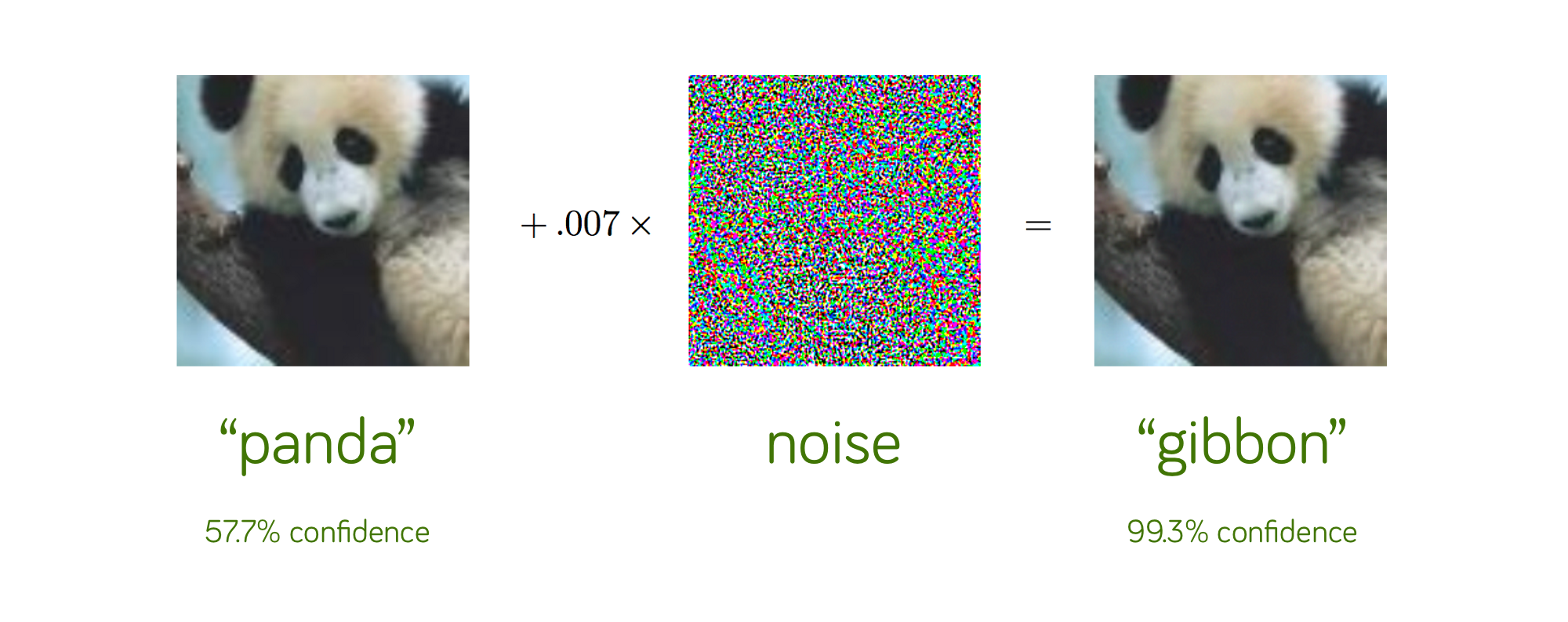
여기서 중점적으로 확인해볼 것은 adversarial attack robustness와 모델이 HFC를 사용하는 경향의 관계성에 대해서 분석합니다. 먼저, 확인해볼것은 convolution kernel의 smoothness와 HFC에 대한 모델의 민감도 사이의 관계를 확인하고 이를 이용해서 대립적으로 강건한(adversarially robust) 모델이 smooth kernel을 가진다는 것을 보이도록 하겠습니다. 여기서 smooth kernel이란 kernel 내의 weight의 dynamic range가 적은 것을 의미합니다.
convolution theorem에 따르면 spatial domain에서 kernel을 이용해서 이미지에 convolution을 취하는 것은 frequency domain에서 원소별 곱을 취하는 것과 동일합니다. 따라서, 만약 spatial domain에서의 kernel weight가 무시할만할 정도로 작으면 frequency domain에서도 HFC가 거의 영향을 주지 않을 것입니다. 따라서 본 논문에서는 모델이 HFC를 무시하도록 강제하는 것은 frequency domain에서 HFC가 거의 영향을 주지 않는 convolution kernel을 배우는 것과 동일하다는 것을 언급하고 있습니다.
기본적으로 kernel의 smoothness와 adversarial robustness를 분석하기 위해서는 모델의 첫번째 layer에 해당하는 convolution kernel을 시각화하는 것이 최선의 방법입니다. 이때, 모델은 adversarial attack을 당하지 않은 vanilla dataset으로 학습한 모델인 $M_{\text{natural}}$과 adversarial attack에 당한 모델인 $M_{\text{adversarial}}$을 모두 확인해봐야합니다. 그 결과는 아래의 그림을 참고하시면 됩니다.
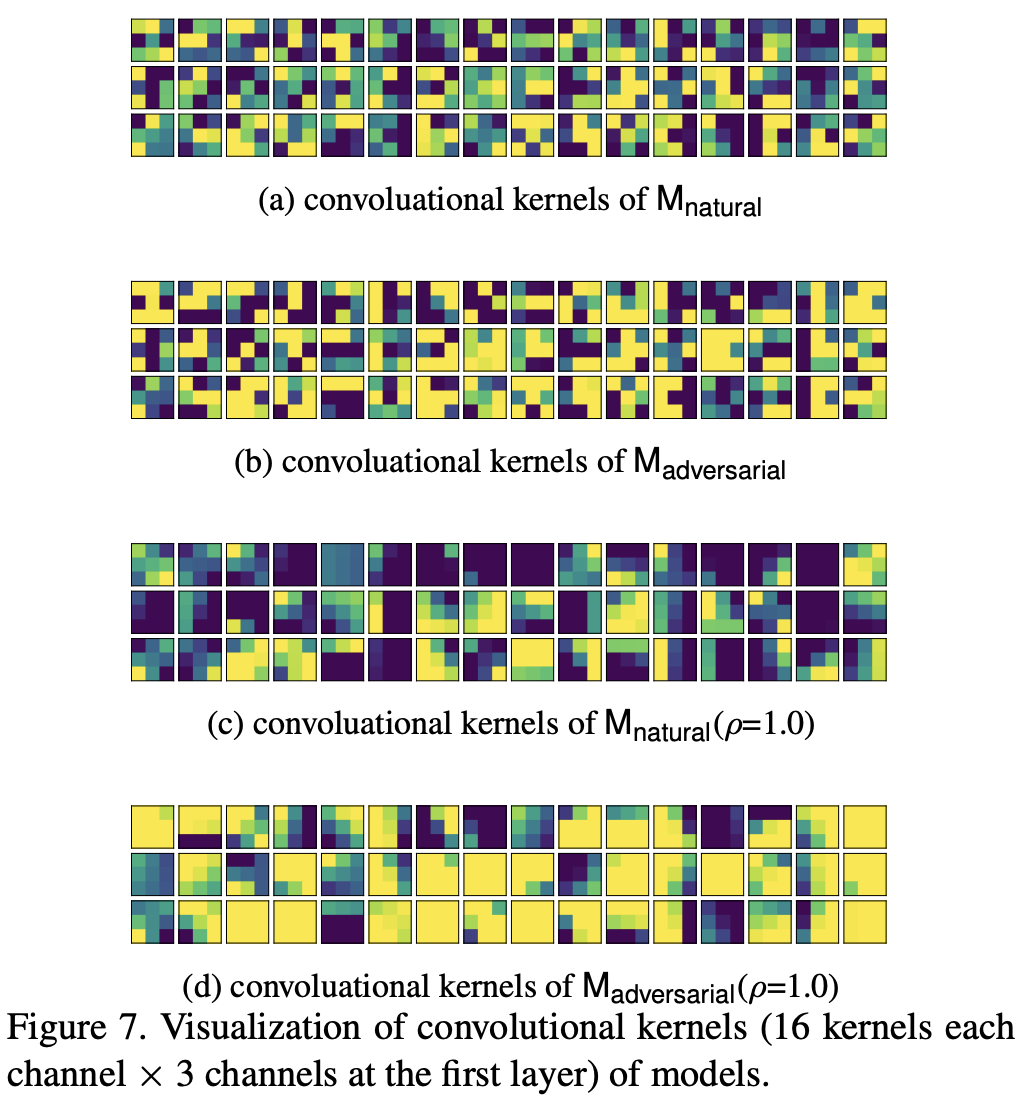
위의 그림에서 (a), (b)를 보시면 $M_{\text{natural}}$의 kernel은 weight 값이 다양한 것을 볼 수 있습니다. 그에 반해 $M_{\text{adversarial}}$는 kernel의 weight가 전체적으로 유사한 것을 볼 수 있습니다.
일단 지금까지 얻은 결과는 $M_{\text{adversarial}}$은 smooth kernel을 갖는 다는 것이였습니다. 그렇다면 smooth kernel이 adversarial attack의 robustness에 어떤 영향을 줄 지 분석해봐야합니다. 이 논문에서는 강제로 kernel의 weight를 smoothing하게 방법을 취하는 데 아래의 수식을 이용합니다.
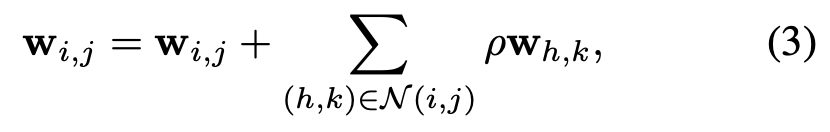
여기서 $\rho$는 하이퍼파라미터입니다. 실제로 Figure 7의 그림에서 (c), (d)를 보면 기존의 결과보다 더 smooth kernel을 얻을 수 있습니다. 이 방법을 사용해서 얻은 결과는 아래의 표를 참고하시면 됩니다.
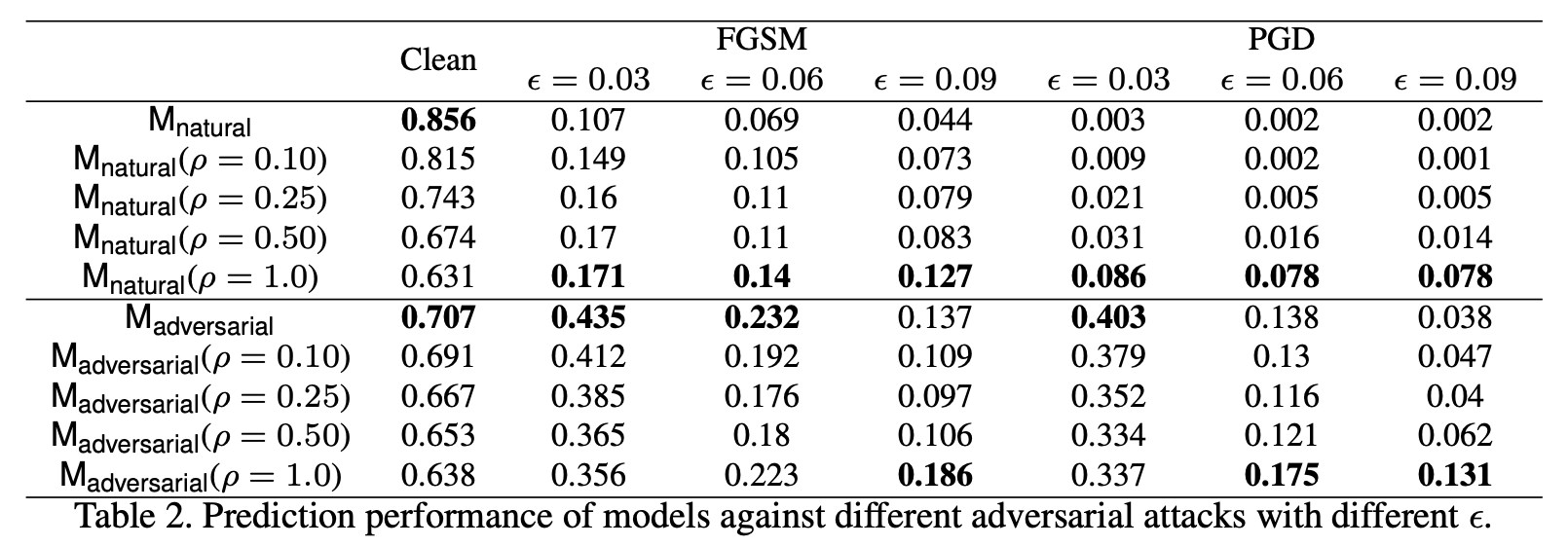
위의 표를 보면 smoothing method를 적용 시 깨끗한 이미지로 학습하게 되면 성능은 떨어지지만, adversarial attack에 대한 robustness는 강화되는 것을 볼 수 있습니다. 비록 $M_{\text{adversarial}}$에 대해서는 robustness의 향상을 두드러지게 볼 수 없으나 perturbation이 큰 경우에는 나름 도움에 되는 것으로 확인할 수 있습니다.
모든 결론을 종합하면 아래와 같습니다.

