지난 포스팅의 [PML intro] Ch7 Linear Algebra (Sec.7.1 Introduction - 1)에서는 선형대수(Linear Algebra)의 기초적인 내용을 다루어보았습니다. 선형대수는 결국 벡터, 행렬, 그리고 텐서를 다루는 학문으로 이를 포함한 집합과 관련된 연산을 정의한 공간이 바로 벡터공간(Vector Space)입니다. 오늘은 이에 대한 간단한 설명을 진행하겠습니다. 혹시 이에 대한 더 자세한 내용이 궁금하신 분은 제가 이전에 포스팅한 글을 참고해주세요.
1. 벡터의 덧셈과 스칼라배 (Vector Addition and Scaling)
벡터 $\mathbf{x} \in \mathbb{R}^{n}$은 $n$차원 유클리드 공간(Euclidean Space)에서 한 점으로 볼 수 있습니다. 벡터공간은 이러한 벡터들의 모임으로 벡터끼리 더하거나 스칼라를 곱해서 새로운 점을 만들 수 있습니다. 이러한 연산들은 원소별(element-wise)로 다음과 같이 자연스럽게 정의할 수 있습니다.
$$\begin{cases} \mathbf{x} + \mathbf{y} &= (x_{1} + y_{1}, \dots, x_{n} + y_{n}) \\ c\mathbf{x} &= (cx_{1}, \dots, cx_{n}) \end{cases}$$
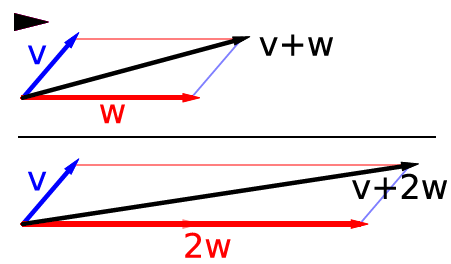
위 그림은 벡터 연산의 예시를 그림으로 보여주고 있습니다.
2. 선형독립 (Linear Independent), 생성공간 (Span), 기저집합 (Basis Set)
벡터 집합 $\{ \mathbf{x}_{1}, \dots, \mathbf{x}_{n} \}$이 선형독립이라는 것은 어떤 벡터도 다른 벡터들의 선형결합(linear combination)으로 표현될 수 없다는 것을 의미합니다. 반대로 나머지 벡터들의 선형결합으로 표현할 수 있다면 이를 선형종속(linear dependent)라고 합니다. 예를 들어, 어떤 계수 $\{ \alpha_{1}, \dots, \alpha_{n - 1} \}$이 존재하여 $\mathbf{x}_{n} = \sum_{i = 1}^{n - 1} \alpha_{i}\mathbf{x}_{i}$라면 $\{ \mathbf{x}_{1}, \dots, \mathbf{x}_{n} \}$는 선형종속입니다.
벡터 집합 $\{ \mathbf{x}_{1}, \dots, \mathbf{x}_{n} \}$의 생성공간은 이 벡터들의 선형결합으로 표현가능한 모든 벡터들의 집합을 의미합니다. 즉 다음과 같이 쓸 수 있죠.
$$\text{span} (\{ \mathbf{x}_{1}, \dots, \mathbf{x}_{n} \}) = \{ \mathbf{v} \mid \mathbf{v} = \sum_{i = 1}^{n} \alpha_{i}\mathbf{x}_{i}, \alpha_{i} \in \mathbb{R} \}$$
또한, $\mathbf{x}_{i} \in \mathbb{R}^{n}$인 서로 선형독립인 $n$개의 벡터 $\{ \mathbf{x}_{1}, \dots, \mathbf{x}_{n} \}$에 대새 선형독립이라면 $\text{span} (\{ \mathbf{x}_{1}, \dots, \mathbf{x}_{n} \}) = \mathbb{R}^{n}$이 됩니다. 즉, $\mathbb{R}^{n}$의 임의의 벡터 $\mathbf{v}$는 벡터 집합 $\{ \mathbf{x}_{1}, \dots, \mathbf{x}_{n} \}$ 내에 포함된 벡터들의 선형결합으로 쓸 수 있다는 것이죠.
기저집합 $\mathcal{B}$는 선형독립이면서 전체공간을 span할 수 있는 벡터들의 집합을 의미합니다. 즉 $\text{span}(\mathcal{B}) = \mathbb{R}^{n}$을 만족합니다. 기저는 여러가지가 있을 수 있으며 표준기저(Standard Basis)는 좌표벡터 $\mathbf{e}_{1} = (1, 0, \dots, 0)$부터 $\mathbf{e}_{n} = (0, 0, \dots, 1)$까지를 사용합니다. 이 표준기저 덕분에 $\mathbb{R}^{2}$의 벡터를 원점에서 시작하는 평면 위의 화살표로 보거나 기저벡터들의 계수로 이뤄진 순서가 있는 숫자 목록으로 볼 수도 있죠.
3. 선형사상(Linear Map)과 행렬
선형사상(linear map) 또는 선형변환(linear transformation) $f: \mathcal{V} \rightarrow \mathcal{W}$는 모든 벡터 $\mathbf{v}, \mathbf{w} \in \mathcal{V}$와 스칼라 $a$에 대해 $f(\mathbf{v} + \mathbf{w}) = f(\mathbf{v}) + f(\mathbf{w})$와 $f(a\mathbf{v}) = af(\mathbf{v})$를 동시에 만족하는 함수입니다.
결국 정의역 $\mathcal{V}$도 벡터공간이기 때문에 기저가 존재하겠죠. 그렇다면 선형사상 $f: \mathcal{V} \rightarrow \mathcal{W}$는 기저벡터들이 어디로 가는 지만 지정하면 완전히 결정됩니다. 왜냐하면 $\mathcal{V}$의 원소들은 기저벡터들의 선형결합으로 유일하게 표현되기 때문입니다.
이제, $\mathcal{V} = \mathbb{R}^{n}$과 $\mathcal{W} = \mathbb{R}^{m}$이라고 두겠습니다. 그러면 $\mathcal{V}$의 각 기저벡터 $\mathbf{v}_{i}$에 대해 $f(\mathbf{v}_{i}) \in \mathbb{R}^{m}$을 계산해 이를 $m \times n$ 행렬 $\mathbf{A}$의 열로 저장하게 됩니다. 그러면 임의의 $\mathbf{x} \in \mathbb{R}^{n}$에 대해 $\mathbf{y} = f(\mathbf{x}) \in \mathbb{R}^{m}$은 다음과 같이 계산됩니다.
$$\mathbf{y} = (\sum_{j = 1}^{n} a_{1j}x_{j}, \dots, \sum_{j = 1}^{n} a_{mj}x_{j})^{T}$$
이는 곧 행렬곱 $\mathbf{y} = \mathbf{A}\mathbf{x}$와 동일하게 되죠. 이때, 이 함수가 가역이라면 $\mathbf{x} = \mathbf{A}^{-1}\mathbf{y}$와 같이 쓸 수 있습니다.
4. 행렬의 치역(range)과 영공간(nullspace)
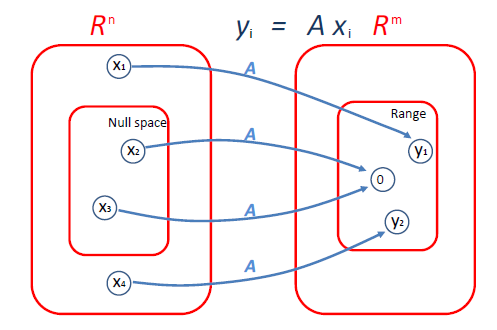
행렬 $\mathbf{A} \in \mathbb{R}^{m \times n}$을 $\mathbb{R}^{m}$ 안의 $n$개의 열벡터라고 보겠습니다. 이때, 행렬의 치역 또는 열공간은 $\mathbf{A}$의 열들이 span하는 공간으로 다음과 같이 정의됩니다.
$$\text{range}(\mathbf{A}) = \{ \mathbf{v} \in \mathbb{R}^{m} \mid \mathbf{v} = \mathbf{A}\mathbf{x}, \mathbf{x} \in \mathbb{R}^{n} \}$$
이는 행렬 $\mathbf{A}$러 만들 수 있는 벡터들의 집합으로 $\mathbb{R}^{m}$의 부분공간이며 그 차원은 행렬 $\mathbf{A}$의 랭크(rank)로 정의됩니다. 반면 행렬 $\mathbf{A} \in \mathbb{R}^{m \times n}$의 영공간은 $\mathbf{A}$를 곱했을 때 영벡터로 매핑되는 모든 벡터들의 집합으로 다음과 같이 정의됩니다.
$$\text{nummspace}(\mathbf{A}) = \{ \mathbf{x} \in \mathbb{R}^{n} \mid \mathbf{A}\mathbf{x} = \mathbf{0} \}$$
5. 선형 사영(Linear projection)
$\mathbf{y} \in \mathbb{R}^{m}$를 $\{ \mathbf{x}_{1}, \dots, \mathbf{x}_{n} \}$의 span에 사영한다는 것은 $\mathbf{y}$에 가장 가까운 (유클리드 노름 기준 $||\mathbf{v} - \mathbf{y}||_{2}$) $\mathbf{v} \in \text{span} (\{ \mathbf{x}_{1}, \dots, \mathbf{x}_{n} \})$을 찾는 것입니다. 이를 $\text{Proj}(\mathbf{y}; \{ \mathbf{x}_{1}, \dots, \mathbf{x}_{n} \})$으로 쓰고 다음과 같이 정의합니다.
$$\text{Proj}(\mathbf{y}, \{ \mathbf{x}_{1}, \dots, \mathbf{x}_{n} \}) = \text{argmin}_{\mathbf{v} \in \text{span}(\{ \mathbf{x}_{1}, \dots, \mathbf{x}_{n} \})} ||\mathbf{y} - \mathbf{v}||_{2}$$
full rank인 $\mathbf{A} \in \mathbb{R}^{m \times n}$이고 $m \ge n$이라고 가정하겠습니다. $\mathbf{y} \in \mathbb{R}^{m}$을 $\mathbf{A}$의 치역으로 사영하게 되면 다음과 같습니다.
$$\text{Proj}(\mathbf{y}, \mathbf{A}) = \text{argmin}_{\mathbf{v} \in \mathcal{R}(\mathbf{A})} ||\mathbf{y} - \mathbf{v}||_{2} = \mathbf{A}(\mathbf{A}^{T}\mathbf{A})^{-1}\mathbf{A}^{T}\mathbf{y}$$
이는 향후에 알아볼 정규방정식(normal equation)의 해와 동일하게 됩니다.
'인공지능 > Probabilistic Machine Learning (intro)' 카테고리의 다른 글
| [PML intro] Ch7 Linear Algebra (Sec.7.1 Introduction - 4) (0) | 2025.12.12 |
|---|---|
| [PML intro] Ch7 Linear Algebra (Sec.7.1 Introduction - 3) (0) | 2025.12.11 |
| [PML intro] Ch7 Linear Algebra (Sec.7.1 Introduction - 1) (0) | 2025.12.09 |
| [PML intro] Ch6 Information Theory (Sec.6.3 Mutual Information - 8) (0) | 2025.12.08 |
| [PML intro] Ch6 Information Theory (Sec.6.3 Mutual Information - 7) (0) | 2025.12.08 |
