안녕하세요. 오늘은 Transformer에 Deformable Convolution Network의 컨셉을 적용한 Deformable Attention Module을 소개하도록 하겠습니다.
Background
Vision Transformer(ViT)는 CNN보다 넓은 수용영역(receptive field)를 통해 장거리 의존성 모델링에 강점을 보이며 영상 분류, 객체 검출 및 분할 등과 같은 다양한 컴퓨터 비전 문제에서 활용되고 있습니다. 하지만 단순히 수용영역을 넓히는 것은 두 가지 문제를 야기합니다.
- Dense Attention의 비효율성: ViT와 같이 모든 쿼리가 전체 키에 접근하는 방식은 연산 및 메모리 비용이 크고 불필요한 정보까지 주목하여 과적합 위험이 높아집니다.
- Sparse Attention의 한계: Swin Transformer나 PVT와 같이 윈도우 기반 또는 다운샘플링 기반의 어텐션 방식은 연산 효율을 높히는 데 도움이 되지만 데이터 비의존적(data-agnostic) 구조라서 중요한 장거리 관계를 놓칠 수 있습니다.
CNN에서는 Deformable Convolution Network(DCN)이 데이터 의존적(data-dependent)으로 수용 영역을 변형해 중요한 영역에 집중하는 성과를 보였습니다. 이러한 특성을 Transformer에서도 적용하려는 시도는 있었으나 대부분은 검출기의 헤드 또는 전처리 모듈 수준에 머물렀고 Transformer 자체 백본 구조에 이를 통합하는 것은 계산량이 너무 과도하였습니다.
본 논문에서는 이러한 한계를 극복하기 위해 Deformable Attention Transformer(DAT)라는 새로운 비전 백본 모델을 제안합니다. 이는 모든 쿼리에 대해 동일한 형태의 레퍼런스 점을 배치하고 쿼리 패치로부터 예측한 오프셋으로 키 및 밸류의 위치를 변형하게 됩니다. 이를 통해 데이터 의존적이면서도 계산 복잡도를 선형으로 유지할 수 있게 되는 것이죠. 또한, Swin Transformer와 유사한 피라미드 구조를 채택하되 마지막 두 개의 스테이지에서만 Deformable Attention을 적용하였습니다. 이는 초반에 Shift-Window Attention을 활용하여 연산량 절약 및 로컬 특징 학습을 강화하겠다는 의미입니다. 실험적으로 DAT는 ImageNet-1K 분류, COCO 객체 검출·인스턴스 분할, ADE20K 시맨틱 분할 등 다양한 벤치마크에서 Swin Transformer 대비 일관된 성능 향상을 달성하였습니다.
Deformable Attention Transformer
1) Preliminary
일반적인 ViT의 어텐션 과정을 복습해보도록 하겠습니다. 입력 데이터는 평탕화된 특성맵으로 $x \in \mathbb{R}^{N \times C}$가 들어옵니다. 여기서 $N = H \times W$은 토큰의 개수이고 $C$의 채널의 개수입니다. 첫번째 단계는 Multi-head Self-Attention(MHSA)입니다. 이는 쿼리 $q = xW_{q}$, 키 $k = xW_{k}$ , 밸류 $v = xW_{v}$ 를 계산하는 것으로 시작합니다. 다음으로 multi-head 구조이기 때문에 입력 채널의 헤드 개수만큼 쪼개서 각 헤드 별로 self-attention을 수행해줍니다.
$$z^{(m)} = \text{Softmax} \left( \frac{q^{(m)} (k^{(m)})^{T}}{\sqrt{d}} \right) v^{(m)}$$
여기서 $d = \frac{C}{M}$입니다. 그리고 각 헤드의 self-attention 결과를 다시 하나로 취합하여 $z = \text{Concat}(z^{(1)}, z^{(2)}, \dots, z^{(M)})W_{o}$를 얻게 됩니다. 그리고 이를 기반으로 전체적인 하나의 Transformer Block이 구성되죠.
$$\begin{cases} &z^{'}_{l} = \text{MHSA}(\text{LN}(z_{l - 1})) + z_{l - 1} \\ &z_{l} = \text{MLP}(\text{LN}(z_{l}^{'})) + z_{l}^{'} \end{cases}$$
여기서 PVT에서는 다운샘플링을 수행하여 연산량을 감소시켜주지만 정보손실이 발생하게 됩니다. 그리고 Swin Transformer에서는 Shifted Window Attention을 적용하였지만 전역 수용영역의 성장 속도가 느려서 큰 객체에 대한 표현력이 제한됩니다. 따라서, 데이터 의존적인 희소 어텐션이 요구될 수 밖에 없습니다.
2) Deformable Attention
그러면 Background에서 설명했던 DCN 컨셉을 바로 Transformer에 도입하면 되지 않을까요? 하지만, 이는 Transformer에서 쿼리의 개수와 키의 개수에 비례하여 이차 복잡도가 발생하여 메모리 및 연산량이 더욱 증가하게 됩니다. 또한, 이전 연구들에 따르면 시각 모델에서 서로 다른 쿼리들에 대응되는 attention map이 유사한 것을 관찰하여 공유된 변형 키/밸류로 효율성을 확보할 수 있음을 언급하였습니다.
따라서, 핵심적인 아이디어로 "Shared Shifted Key/Value"입니다. 이는 모든 쿼리가 동일한 변형된 포인트 집합을 사용하는 것입니다. 이를 통해 효율성과 표현력을 더욱 향상시킬 수 있죠. 그리고 DCN에서 활용한 offset network를 여기에서 적용하게 됩니다. 이는 쿼리 토큰이 입력으로 제공되어 출력으로 참조점에 대한 2D 오프셋를 줍니다. 구조는 $5 \times 5$ DW Convolution + GELU + $1 \times 1$ Convolution으로 구성되어 있습니다. 그러면 얻은 2D 오프셋을 기반으로 Bilinear Interpolation을 적용하여 변형된 위치에서 특징 샘플링 후, 키와 밸류를 생성하게 됩니다.

그림 2는 위에서 언급한 과정을 도식화하였습니다. 전체적인 구성은 분석해보도록 하겠습니다.
2-1) Overall Process
STEP1. 참조점을 생성하기 위해 입력 특징 맵 $H \times W$를 $r$배만큼 다운샘플링하여 $H_{G} \times W_{G}$ 크기의 그리드를 만들고 이를 좌표범위를 $[-1, 1]$로 정규화해줍니다. 예를 들어보겠습니다. $H = W = 14$라고 가정하겠습니다. 그리고 다운샘플링 비율은 $r = 2$라고 했을 때 $H_{G} = W_{G} = 14 / 2 = 7$이 됩니다. 그러면 총 $7 \times 7$ 그리드로 총 49개의 참조점을 생성하게 됩니다. 그리고 정규화는 $x_{\text{norm}} = \frac{2x}{H_{G} - 1} - 1$과 $y_{\text{norm}} = \frac{2y}{H_{G} - 1} - 1$를 적용하여 수행하게 됩니다. 그러면 $(0, 0) \rightarrow (-1, -1)$이 되고 $(3, 3) \rightarrow (0, 0)$이 됩니다.
STEP2. 다음은 오프셋을 만들어주면 됩니다. 참조점 + $\Delta p$가 곧 변형 포인트가 됩니다. 즉, $\Delta p = \theta_{\text{offset}} (q)$가 입니다. 하지만, 너무 크게 변형되지 않게 조절하기 위해 scale factor $s$를 적용하여 $\Delta p \leftarrow s \cdot \text{tanh}(\Delta p)$를 적용하여 최종 변형 정도를 조절합니다.
STEP3. 그리고 변형 위치에서 특징을 샘플링하여 변형 키 $\tilde{k}$와 변형 밸류 $\tilde{v}$를 만들어줍니다. 예를 들어보겠습니다. $H = W = 4$ 그리고 채널 수는 $C = 3$이라고 하겠습니다. 그리고 다운샘플링 비율로 $r = 2$로 정의하면 $H_{G} = W_{G} = 4 / 2 = 2$가 되어 총 4개의 참조점을 가진다고 가정하겠습니다. 쉽게 보기 위해 참조점 하나만 고려해보겠습니다. $(p_{x}, p_{y}) = (1, 2)$이 입력 좌표 그리고 오프셋 $\Delta p = (+0.2, +0.7)$이라고 하면 변형된 포인트는 $p^{'} = (1.2, 1.7)$이 됩니다. 다음 단계는 이전에 리뷰한 DCN과 동일한 방식으로 해당 좌표를 중심으로 Bilinear Intepolation을 적용하면 됩니다.
STEP4. 변형된 점을 중심으로 얻은 키 $\tilde{k}$와 밸류 $\tilde{v}$를 다음과 같이 얻을 수 있습니다.
$$\begin{cases} \tilde{k} &= \tilde{x} W_{k} \\ \tilde{v} &= \tilde{x} W_{v} \end{cases}$$
여기서 $\tilde{x}$는 변형된 좌표로부터 Bilinear Intepolation을 통해 얻은 특징맵입니다.
STEP5. 그리고 변형된 키와 밸류 그리고 Relative Positional Encoding을 적용하여 self-attention을 수행합니다.
$$z^{(m)} = \text{Softmax} \left( \frac{q^{(m)} (\tilde{k}^{(m)})^{T}}{\sqrt{d}} + \phi(\hat{B}; R) \right) \tilde{v}^{(m)}$$
여기서 $\phi(\hat{B}; R) \in \mathbb{R}^{HW \times H_{G}W_{G}}$는 상대적 위치 인코딩을 위한 좌표 행렬로 변형 포인트를 기반으로 상대적인 좌표를 계산하고자 적용됩니다. 기존의 위치 정보 테이블 $\hat{B}$에서 보간하여 위치 바이어스를 생성해줍니다.
2-2) Offset Generation and Offset Group
여기서 Offset Network는 쿼리 특징 $q$로부터 각 참조점에 대해서 오프셋을 추정합니다. 그리고 각각의 참조점은 $s \times s$ 만큼의 영역을 커버하게 되죠. 따라서, Offset Network은 지역적인 위치 정보를 이해하기 때문에 보다 의미있는 오프셋을 제공할 수 있다는 것을 알 수 있습니다.
일반적인 ViT에서의 self-attention은 multi-head를 도입하여 더욱 높은 표현력을 달성하게 설계됩니다. 본 논문 역시 이러한 offset 생성을 각 head 별로 수행하여 다양한 특징을 얻을 수 있도록 돕게 됩니다.
3) Model Architecture
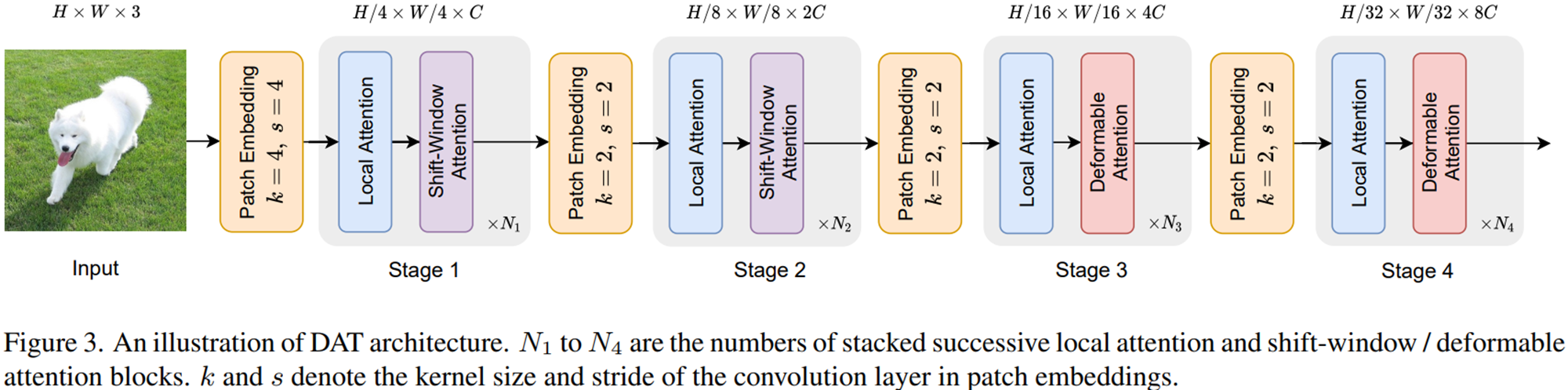
- Backbone 구조: 본 논문에서는 표준 MHSA 대신 Deformable Attention + MLP로 블록 구성하게 됩니다. 이를 통해 데이터 의존적(Adaptive) attention을 수행하여 중요한 위치에만 집중할 수 있게 만들었죠. 또한, 피라미드 구조로 다단계 다운샘플링으로 멀티 스케일 특성맵 생성하여 분류, 객체 검출, 시맨틱 분할 등 다양한 태스크에 활용 가능하게 만들었습니다.
- 입력 처리 과정: 입력 영상은 $H \times W \times 3$라고 가정하고 패치 임베딩을 먼저 적용합니다. 이는 $4 \times 4$ 커널 및 stride 4를 기반으로 구성된 합성곱으로 이루어집니다. 그러면 초기 임베딩은 $\frac{H}{4} \times \frac{W}{4} \times C$가 되고 각 스테이지가 전환될 때마다 $2 \times 2$ 커널 및 stride 2를 기반으로 구성된 합성곱을 적용하여 채널 수는 2배씩 늘리고 공간 크기는 절반씩 줄여주게 됩니다.
- 스테이지 구성: 총 4개의 스테이지로 구성되어 있으며 1번과 2번 스테이지는 Swin Transformer의 Shifted Window Attention을 적용하여 3번과 4번 스테이지에서는 본 논문에서 제안하는 Deformable Attention Module을 적용합니다. 이 설계 덕분에, 초반에는 가볍게 로컬 특징을 잡고 후반에는 전역 컨텍스트까지 고려한 강력한 표현을 학습합니다.
- 태스크 별 활용: 영상 분류의 경우 Stage 4 출력 → 글로벌 풀링 → 선형 분류기의 순서로 적용되고 객체 검출 및 의미론적 분할에 적용한다면 모든 스테이지 출력 → 정규화 → FPN, 디코더 등 후속 모듈에 전달하게 됩니다.
- 모델 변형

Experiment Results
1) Classification Results

2) Object Detection

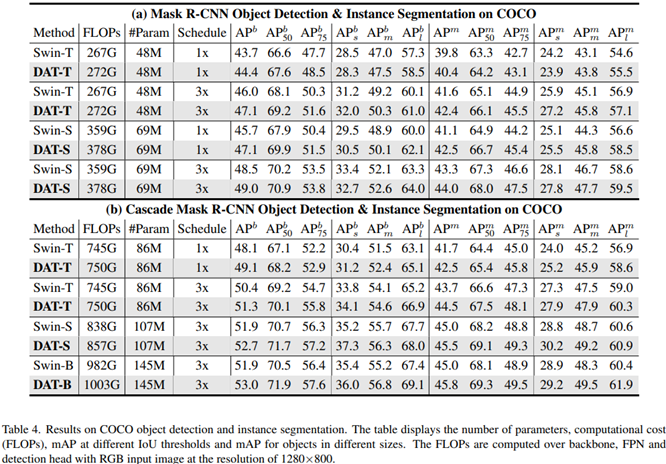
3) Semantic Segmentation

4) Ablation Study
4-1) Geometric Informatoin Exploration
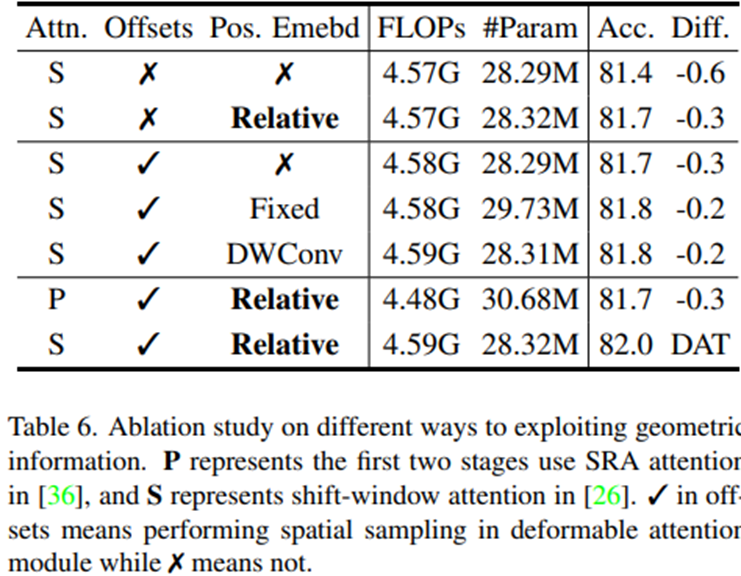
4-2) Deformable attention at different stages

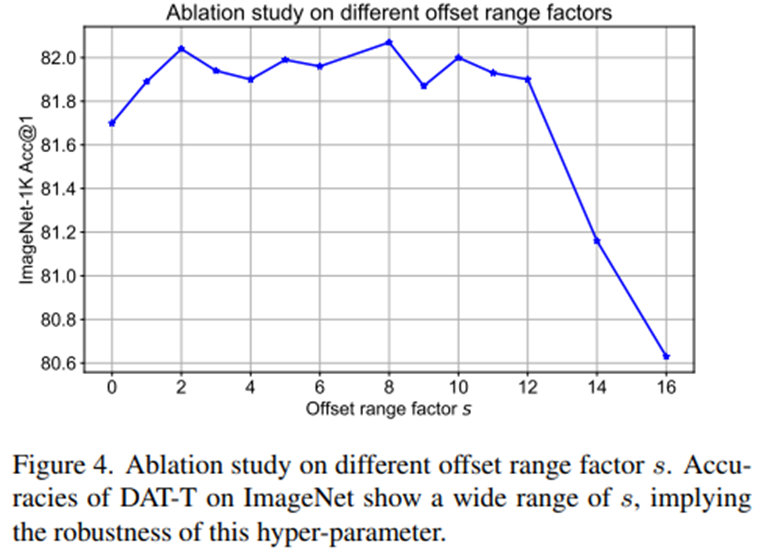
4-3) Ablation on different Offset range scale factor $s$
5) Feature Visualization

