핵심 포인트
- 정렬 알고리즘 (삽입정렬과 거품정렬)
제출코드 (삽입정렬)
N = int(input())
numbers = [int(input()) for _ in range(N)]
for i in range(1, N):
key = numbers[i]
for j in range(i-1, -1, -1):
if numbers[j] > key: numbers[j+1] = numbers[j]
else:
j += 1
break
numbers[j] = key
print(*numbers, sep='\n')제출코드 (거품정렬)
N = int(input())
numbers = [int(input()) for _ in range(N)]
for i in range(0, len(numbers)):
for j in range(0, len(numbers)-1):
if numbers[j] > numbers[j + 1]:
temp = numbers[j + 1]
numbers[j + 1] = numbers[j]
numbers[j] = temp
print(*numbers, sep='\n')해설
오늘부터 본격적으로 정렬 알고리즘을 이용한 문제들을 풀어보도록 하겠습니다. 본 코드 제출을 삽입정렬과 거품정렬로 두 가지 방식으로 제출할 수 있으니 두 방법에 대해서 모두 알아보도록 하겠습니다.
1). 삽입정렬 (Insert Sorting)
삽입정렬은 이름에서도 보이다싶이 어떤 값이 들어갈 위치를 찾아 그 위치에 값을 "삽입"하는 과정입니다. 그림을 통해 보시면 더욱 쉽게 이해할 수 있습니다.

위와 같이 9, 1, 5, 8, 2의 정렬이 되지 않은 숫자들이 입력되었다고 가정하겠습니다. 삽입정렬을 위해서는 제일 먼저 키값을 지정해주어야합니다.
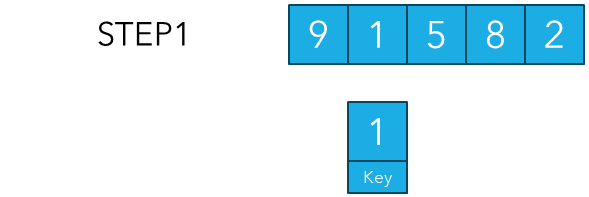
위와 같이 기본적으로 삽입정렬에서는 가장 처음에 알고리즘 수행 시 0번째 인덱스 값은 이미 정렬이 되었다고 가정하기 때문에 1번째 인덱스에 해당하는 값인 1을 키값으로 지정해줍니다.
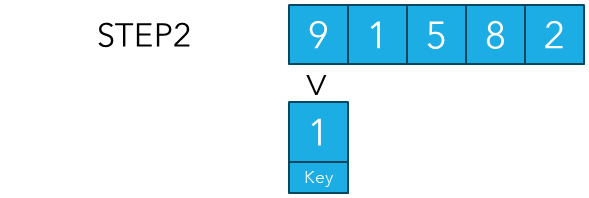
다음으로 현재 저희는 1번째 인덱스를 키값으로 잡았기 때문에 역순으로 0번째 인덱스와 키값을 비교합니다. 이때, 오름차순으로 정렬하기 때문에 키값이 해당 인덱스값보다 작다면 0번째 인덱스값을 1번째 인덱스로 옮겨줍니다.
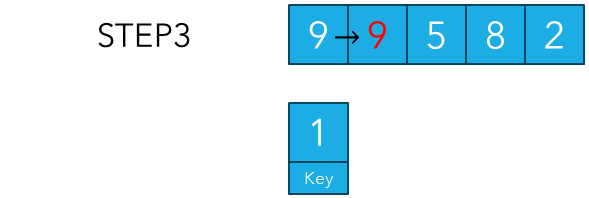
그러면 위 그림에서 빨간색 9와 같이 기존에 1이였던 값이 9로 덮혀씌워지게 됩니다. 이 과정이 곧 1이 들어갈 적당한 자리를 찾기 위해 앞에 있는 더 큰 숫자들을 한 칸씩 뒤로 밀어주는 과정을 의미합니다.
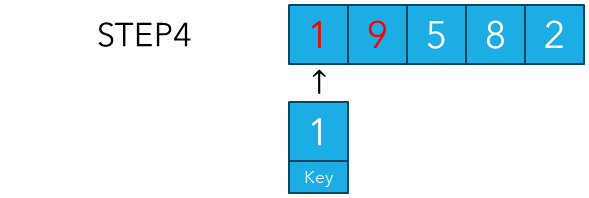
그리고 아까 저장해놓았던 키값을 해당 자리에 삽입해주면 1번째 인덱스에 대한 정렬이 종료됩니다. 이제 2~4번째 인덱스까지 위 과정을 쭉 반복하면 됩니다.

위 과정을 모든 인덱스에 대해서 반복하면 다음과 같은 그림을 그려볼 수 있습니다.
제가 삽입정렬을 이용해서 제출한 코드 역시 이와 동일한 방식으로 진행됩니다. 보시면 i는 1번 인덱스부터 시작해서 입력 시퀀스의 개수만큼 반복하게 됩니다. 그리고 i번째 인덱스에 해당하는 값인 numbers[i]를 key에 저장하죠. 다음으로 i - 1부터 0까지 역순으로 key가 들어갈 위치를 찾습니다. 이를 위해 key 보다 더 큰 값들은 numbers[j + 1] = numbers[j]로 한 칸씩 밀어줍니다. 위 그림에서도 보이다 샆이 j를 이용해서 순회하다보면 key 가 들어갈 인덱스보다 한 칸 더 전진합니다. 따라서, 코드 상에서는 j += 1을 통해 다시 원래 들어갈 위치로 바꾸어줍니다. 다음으로 numbers[j] = key 를 통해 해당 위치에 key 를 삽입해줍니다.
2). 거품정렬 (Bubble Sorting)
거품정렬의 기본원리는 삽입정렬보다 쉽습니다. 거품정렬은 i번째 인덱스값과 i+1번째 인덱스값을 비교한 뒤 i번째 인덱스값이 더 크면 두 값을 교환하고 아니면 다음 인덱스로 넘어가 비교를 수행합니다.

이번에도 위와 같이 9, 1, 5, 8, 2의 정렬이 되지 않은 숫자들이 입력되었다고 가정하겠습니다.
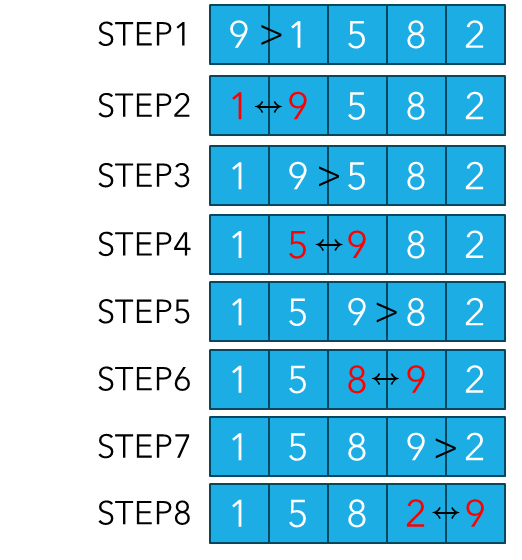
위 그림은 0번째 인덱스값부터 시작하여 바로 다음 인덱스인 1번째 인덱스랑 비교하는 하는 것부터 시작하는 거품정렬의 1회 주기를 보여주고 있습니다. 최종적으로 9는 바로 다음 인덱스값보다 항상 컸기 때문에 계속 뒤로 밀려나서 마지막 인덱스에 위치하는 것을 볼 수 있죠. 따라서, 거품정렬이 한번 수행되면 마지막 인덱스는 이미 정렬된 상황이라고 볼 수 있습니다. 이 과정을 모두 정렬될 때 까지 반복하면 됩니다.

위 과정을 모든 인덱스에 대해서 반복하면 다음과 같은 그림을 그려볼 수 있습니다. 코드는 매우 간단하기 때문에 따로 설명은 하지 않도록 하겠습니다.
참고자료 및 그림출처
'Programming > Coding Problem' 카테고리의 다른 글
| BOJ 25305번: 커트라인 (0) | 2024.01.01 |
|---|---|
| BOJ 2587번: 대표값 2 (0) | 2023.12.31 |
| BOJ 1436번: 영화감독 숌 (0) | 2023.07.04 |
| BOJ 19532번: 수학은 비대면강의입니다 (0) | 2023.07.02 |
| BOJ 24313번: 알고리즘 수업 - 점근적 표기 1 (0) | 2023.07.01 |
