안녕하세요. 지난 포스팅의 디지털 영상 처리 - 2 변수 함수로의 확장에서는 기존의 1D DFT를 2D DFT로의 확장을 해보았습니다. 또한 1D 샘플링 정리를 2D 샘플링 정리로도 확장을 해보았습니다. 결론적으로는 1D나 2D나 그렇게 큰 차이는 없다는 것입니다. 그저 변수가 하나 더 추가되었다는 점이죠. 오늘은 2D DFT의 더 많은 특성들을 알아보도록 하겠습니다. 소개할 몇몇 특성들은 이후에 디지털 영상 처리에 있어서 중요한 역할을 하기 때문에 알아두는 것이 중요합니다.
1. 공간 및 주파수 간격들간의 관계
혹시 디지털 영상 처리 - 단일 변수 함수의 이산 푸리에 변환(Discrete Fourier Transform)에서 샘플링과 주파수 간격 사이의 관계식을 기억하시나요. 다시 간단하게 정리하면 $\Delta T$ 간격으로 샘플링이 취해진 함수 $f(t)$가 있다고 가정하겠습니다. 총 $M$개의 샘플로 이루어졌다고 했을 때, 샘플링된 전체 구간은 $T = M\Delta T$가 됩니다. 해당 샘플의 DFT에 대응되는 주파수 공간에서도 총 $M$개의 샘플로 이루어져 있다고 가정했을 때 샘플 간 간격은 $\Delta \mu = \frac {1}{M\Delta T} = \frac {1}{T}$라고 볼 수 있습니다. 따라서 주파수 공간에서 샘플링된 전체 구간은 $\Omega = M\frac {1}{T} = \frac {1}{\Delta T}$임을 알 수 있습니다. 이에 대해 크게 2가지로 해석할 수 있습니다.
- $\Delta \mu = \frac{1}{T} \Rightarrow $ DFT의 주파수 공간에서의 해상도는 신호 공간에서 샘플링된 전체 구간 $T$에 의존합니다.
- $\mu = \frac{1}{\Delta T} \Rightarrow $ DFT의 주파수 공간에서의 샘플링된 전체 구간은 신호 공간에서의 해상도 $\Delta T$에 의존합니다.
이와 유사하게 2D DFT도 마찬가지의 특성을 가집니다. 연속 함수 $f(t, z)$를 각각 $t$ 방향과 $z$ 방향으로 샘플링하여 $M \times N$ 개의 샘플들로 구성된 디지털 영상 $f(x, y)$를 만든다고 가정하겠습니다. $\Delta T$와 $\Delta Z$는 각 방향의 샘플들 간의 간격을 나타낸다고 가정하겠습니다. 그러면 주파수 공간에서 두 가지 방향에 따른 샘플링 간격 $\Delta \mu, \Delta \nu$ 사이의 관계는 아래와 같습니다.
$$\Delta \mu = \frac{1}{M\Delta T}, \Delta \nu = \frac {1}{N\Delta Z}$$
즉, 주파수 공간에서의 샘플들 간의 간격은 공간 샘플들 간의 간격과 샘플 수에 모두 반비례한다는 것입니다. 또한 각 방향에서 $T = M\Delta T, Z = N\Delta Z$를 만족하기 때문에 신호 공간에서 샘플링된 전체 구간에 반비례하다고도 볼 수 있습니다.
2. 이동과 회전
먼저 DFT가 입력 함수가 평행 이동을 하는 경우 어떤 결과를 보여주는 지 알아보도록 하겠습니다. 일단 $x$ 방향으로는 총 $M$개, $y$ 방향으로는 총 $N$개의 샘플 값을 가지고 있는 $f(x, y)$가 있다고 가정하겠습니다. 그러면 이전 포스팅에서 보았던 2D DFT 쌍의 관계에 의해서 저희는 아래와 같은 관계식을 가지게 됩니다.
$$F(\mu, \nu) = \sum_{x = 0}^{M - 1}\sum_{y = 0}^{N - 1} f(x, y)e^{-j2\pi\left(\frac{\mu x}{M} + \frac {\nu y}{N}\right)}$$
$$f(x, y) = \frac{1}{MN}\sum_{\mu = 0}^{M -1}\sum_{\nu = 0}^{N - 1} F(\mu, \nu) e^{j2\pi\left(\frac {\mu x}{M} + \frac {\nu y}{N}\right)}$$
저희는 아래의 변환쌍들을 각각 증명해보도록 하겠습니다.
$$f(x, y)e^{j2\pi\left(\frac{\mu_{0}x}{M} + \frac {\nu_{0} y}{N}\right)} \Leftrightarrow F(\mu - \mu_{0}, \nu - \nu_{0})$$
$$\mathcal {F}\{f(x, y) e^{j2\pi\left(\frac {\mu_{0} x}{M} + \frac {\nu_{0} y}{N}\right)}\} = \sum_{x = 0}^{M - 1} \sum_{y = 0}^{N - 1} \left [f(x, y) e^{j2\pi\left(\frac {\mu_{0} x}{M} + \frac {\nu_{0} y}{N}\right)}\right] e^{-j2\pi\left(\frac {\mu x}{M} + \frac {\nu y}{N}\right)}$$
$$ = \sum_{x = 0}^{M - 1} \sum_{y = 0}^{N - 1} f(x,y) e^{-j2\pi\left(\frac{(\mu - \mu_{0})x}{M} + \frac{(\nu - \nu_{0})y}{N}\right)}$$
$$ = F(\mu - \mu_{0}, \nu - \nu_{0})$$
$$f(x - x_{0}, y - y_{0}) \Leftrightarrow F(\mu, \nu)e^{-j2\pi\left(\frac{x_{0}\mu}{M} + \frac {y_{0}\nu}{N}\right)}$$
$$\mathcal {F}^{-1}\{F(\mu, \nu) e^{-j2\pi\left(\frac {x_{0}\mu}{M} + \frac {y_{0} \nu}{N}\right)}\} = \left [\frac {1}{MN} \sum_{\mu = 0}^{M - 1} \sum_{\nu = 0}^{N - 1} F(\mu, \nu) e^{j2\pi\left(\frac {x\mu}{M} + \frac {y\nu}{N}\right)}\right] e^{-j2\pi\left(\frac {x_{0}\mu}{M} + \frac {y_{0}\nu}{N}\right)}$$
$$ = \left [\frac {1}{MN} \sum_{\mu = 0}^{M - 1} \sum_{\nu = 0}^{N - 1} F(\mu, \nu) e^{j2\pi\left(\frac{(x - x_{0})\mu}{M} + \frac{(y - y_{0})\nu}{N}\right)}\right]$$
$$ = f(x - x_{0}, y - y_{0})$$
첫 번째 수식을 자세히 보시면 지수 함수를 $f(x, y)$에 곱하면 DFT의 원점이 $(\mu_{0}, \nu_{0})$로 이동됩니다. 또 두 번째 수식도 지수 함수를 $F(\mu, \nu)$에 곱하면 $f(x, y)$의 원점이 $(x_{0}, y_{0})$로 이동됩니다. 또한 평행 이동은 $F(\mu, \nu)$의 크기, 즉 스펙트럼에 어떠한 영향도 주지 않는다는 것을 볼 수 있습니다. 따라서 이동 연산은 DFT의 푸리에 스펙트럼에 있어 "불변성"을 갖는 다고 할 수 있습니다.
이러한 특성은 회전에도 적용됩니다. 회전에 대한 불변성을 증명하기 위해서 극좌표(polar coordinate)로 바꾸어보도록 하겠습니다.
$$x = r\cos {\theta}, y = r\sin {\theta}, \mu = \omega\cos {\phi}, \nu = \omega\sin {\phi}$$
그리고 $\theta_{0}$만큼 회전시켰다고 가정하면 $f(r, \theta + \theta_{0}) \Leftrightarrow F(\omega, \phi + \theta_{0})$의 DFT 변환 쌍을 가지게 됩니다. 즉, 영상 공간에서 $\theta_{0}$만큼 회전이 되면 주파수 공간에서도 $\theta_{0}$만큼 회전이 됩니다.
3. 주기성
1D와 마찬가지로 2D DFT와 IDFT 역시 $\mu, \nu$ 방향으로 주기적으로 무한히 반복됩니다. 이를 수학적으로 표기하면 아래와 같이 쓸 수 있습니다.
$$F(\mu, \nu) = F(\mu + k_{1} M, \nu) = F(\mu, \nu + k_{2}N) = F(\mu + k_{1}M, \nu + k_{2} N)$$
$$f(x, y) = f(x + k_{1} M, y) = F(x, y + k_{2}N) = F(x + k_{1}M, y + k_{2} N)$$
이때, $k_{1}, k_{2}$는 모두 정수입니다. DFT와 IDFT의 주기성은 알고리즘 구현 시 매우 중요한 사항이 되기 때문에 잘 알아두셔야 합니다. 그림을 통해서 그 중요성을 알아보도록 하겠습니다.

기본적으로 1D DFT를 적용하게 되면 변환의 중심은 원점이 되고 이러한 주기가 $M$이 될 때마다 반복됩니다. 이 부분은 이미 설명드렸습니다. 그렇다면 원점을 중심으로 가지는 1주기 $P_{0}$와 $M$을 중심으로 가지는 2주기 $P_{M}$이 맞닿는 지점은 어디일까요? 바로 $\frac {M}{2} - 1$과 $\frac {M}{2}$ 사이에서 만나게 될 것입니다. 저희가 만약 DFT의 결과를 시각화 또는 중심 영역을 필터링해본다고 가정하겠습니다. 그렇다면 저희는 완전한 한 개의 주기 $P_{0}$이나 $P_{M}$을 추출해내야 합니다. 그런데 $P_{0}$을 추출하려고 봤더니 정의역이 음수에 걸쳐서 선택하기 애매합니다. 그렇다면 $P_{M}$을 선택해볼까요? 하지만 $P_{M}$ 역시 저희가 가지고 있는 전체 샘플의 개수인 $M$ 이상으로 넘어가기 때문에 이 역시 그리 좋은 선택은 아니라고 볼 수 있습니다. 그러므로 저희의 유일한 선택지는 $[0, M-1]$ 구간을 추출하는 방법밖에 없습니다. 그러면 $P_{0}$과 $P_{M}$의 반주기가 추출되었다고 볼 수 있겠죠. 그러나 여전히 불안정합니다. 왜냐하면 애초에 완벽한 한 주기를 선택해야 하는 데 반주기씩 선택했으니까요.

이러한 문제를 해결하는 방법이 바로 $P_{0}$의 중심인 원점을 $\frac {M}{2}$만큼 이동하자는 겁니다. 그러면 단순한 평행 이동만으로도 구간 $[0, M - 1]$까지의 완벽한 주기 한 세트를 얻을 수 있습니다. 이때, 저희가 미리 증명했던 DFT의 이동 특성인 $f(x) e^{j2\pi\frac {\mu_{0} x}{M}} \Leftrightarrow F(\mu - \mu_{0})$를 이용할 수 있습니다. 저희가 지수함수 $e^{j2\pi\frac {\mu_{0} x}{M}}$을 곱하면 주파수 공간에서는 $\mu_{0}$만큼 평행이동 하기 때문에 $\mu_{0} = \frac{M}{2}$로 정하면 저희가 원하는 그림대로 원점에서 $\frac{M}{2}$로 중심이 이동하게 되는 것이죠. 따라서 지수항은 $e^{j2\pi\frac{\mu_{0}x}{M}} = e^{j\pi x} = (-1)^{x}$가 되기 때문에 평행 이동시킨 DFT 변환 쌍을 아래와 같이 쓸 수 있습니다.
$$f(x)(-1)^{x} \Leftrightarrow F(\mu - \frac {M}{2})$$
이번에는 2D DFT를 고려해보도록 하겠습니다.
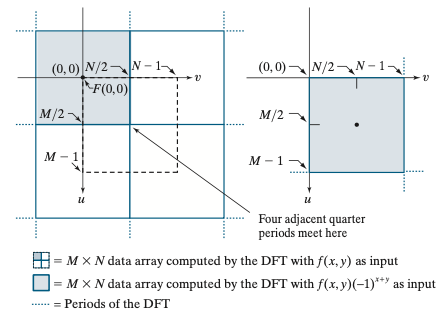
1D와 유사하게 원점 $(0, 0)$을 중심으로 주기가 반복되기 때문에 저희가 원하는 완벽한 주기를 $[0, M - 1] \times [0, N - 1]$에서 선택할 수 없습니다. 따라서 저희는 주기의 중심을 $\mu$ 방향으로는 $\frac {M}{2}$, 그리고 $\nu$ 방향으로는 $\frac{N}{2}$ 만큼 이동하면 완벽한 주기를 추출할 수 있게 됩니다. 아주 간단하죠? 따라서 저희는 $\mu_{0} = \frac{M}{2}$, 그리고 $\nu_{0} = \frac {N}{2}$로 결정하면 저희가 원하는 이동 변환인 $e^{j2\pi\left(\frac {\mu_{0} x}{M} + \frac {\nu_{0} y}{N}\right)} = e^{j\pi(x + y)} = (-1)^{(x + y)}$를 얻을 수 있습니다. 따라서 평행 이동시킨 2D DFT 변환 쌍을 아래와 같이 쓸 수 있습니다.
$$f(x, y)(-1)^{(x + y)} \Leftrightarrow F(\mu - \frac {M}{2}, \nu - \frac {N}{2})$$
'image processing' 카테고리의 다른 글
| 디지털 영상 처리 - 주파수 공간 필터링 기초 (0) | 2021.04.13 |
|---|---|
| 디지털 영상 처리 - 2D DFT 특성 2 (0) | 2021.04.11 |
| 디지털 영상 처리 - 2변수 함수로의 확장 (1) | 2021.04.07 |
| 디지털 영상 처리 - 이산 푸리에 변환과 이산 역푸리에 변환 구현 (0) | 2021.04.07 |
| 디지털 영상 처리 - 단일 변수 함수의 이산 푸리에 변환(Discrete Fourier Transform) (0) | 2021.04.05 |
