안녕하세요. 오늘은 지난 시간의 기초통계학[6].이산확률변수의 분산(https://everyday-image-processing.tistory.com/11)에 이어서 연속확률변수에 대해 알아보겠습니다.
1. 미적분학
이제 이산확률변수가 아닌 연속확률변수로 주제가 바뀌었습니다. 이산확률변수에서 확률을 계산하기 위해 $\sum$을 사용했다면 연속확률변수에서는 확률을 계산하려면 $\int$을 사용합니다. 따라서 본격적으로 연속확률변수에 대해서 알아보기전에 간단한 미적분학 개념을 설명하겠습니다.(이후에 시간이 된다면 미적분학을 포스팅하겠습니다.) 참고로 고등학교 때 배우는 이과 미적분학으로도 충분합니다.(제가 고등학교다닐 때는 문이과가 나뉘어져있었는데 최근에는 문이과 통합이라고 들었습니다...)
기본적으로 어떤 함수를 적분한다는 것은 함수의 밑부분의 넓이를 구한다라는 말입니다. 따라서, $\int_{a}^{b} f(x) \; dx$는 $y=f(x)$의 $[a, b]$구간의 밑부분의 넓이($=area$)와 같습니다.
또한 개념적으로 적분은 합($\sum$)과 같습니다. 그러므로 $\int_{a}^{b} f(x) \; dx$는 $f(x) dx$의 합과 같습니다.
위 두 개념을 하나로 합치면 $area \approx sum\ of\ retangle\ areas=f(x_{1})\Delta x + f(x_{2})\Delta x + \dots + f(x_{n})\Delta x=\sum_{i=1}^{n} f(x_{i})\Delta$입니다. 이를 도식화하면 아래의 그림과 같습니다.
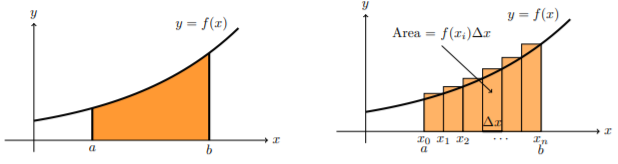
이제 $\Delta x$를 굉장히 작게 줄이면 오른쪽 영역은 왼쪽 영역과 거의 비슷하고 언젠가는 차이가 0에 가까워질것입니다. (미적분학에서는 이런 무한, 극한의 개념을 이해하는 것이 중요합니다.)
2. 연속확률변수(Continuous Random Variables)과 확률 밀도 함수(Probability Density Functions; pdf)
연속확률변수는 이산확률변수와 다르게 범위로 주어집니다. 이 범위는 일반적으로 $[0, 1]$, $(0, \infty)$와 같이 무한한 원소를 포함합니다. 그 이유는 잠시 뒤에 소개됩니다.
-연속확률변수 : $c \le d$를 만족하는 상수 $c$, $d$에 대해서 $P(c \le X \le d) = \int_{c}^{d} f(x) \; dx$인 $f(x)$가 존재한다면 확률 변수 $X$는 연속확률변수라고 합니다. 또한 이러한 $f(x)$는 확률 밀도 함수(pdf)라고 합니다. 이때, 확률 밀도 함수는 1. $f(x) \ge 0$, 2. $ \int_{-\infty}^{\infty} f(x) \; dx=1$를 만족해야합니다.
저희가 이전에 이산확률변수의 확률 질량 함수($p(x)$)를 다루었던 것과 같이 거의 비슷하지만 가장 큰 차이점이 있습니다. 먼저, $p(x)$와는 다르게 $f(x)$는 확률을 의미하지 않습니다. 연속확률변수에서의 확률은 $f(x)$의 특정 범위를 적분해야 얻을 수 있습니다. $f(x)$가 확률이 아니기 때문에 $f(x)$가 반드시 1보다 작거나 같아야한다는 제약조건은 없어지게 됩니다.
연속확률변수에서의 확률을 그림으로 표현하면 아래와 같습니다.
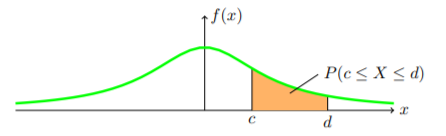
이때, $P(c \le X \le d)$는 초록색 그래프에서 $[c, d]$ 범위 내의 밑부분의 넓이를 의미합니다.
2.1. 확률 질량과 확률 밀도
이산확률변수에서도 뜬금없이 질량이라는 단어가 언급되었습니다. 이전에는 통계에서 질량은 확률이라고 했습니다. 이번에는 밀도라는 단어가 언급되었군요. 어째서 pmf를 설명할 때는 질량, pdf를 설명할 때는 밀도라는 단어를 사용하는 것일까요? 일단 여기서 쓰이는 질량과 밀도는 기본적으로 물리에서 보는 질량과 밀도의 정의와 완벽하게 일치한다는 점에 유의해주시길 바랍니다.
먼저 질량에 대해서 설명하자면 아래의 그림과 같이 질량이 $m_{1}, m_{2}, m_{3}, m_{4}$인 물체가 있다고 가정하겠습니다.

그렇다면 전체 질량은 $m_{1} + m_{2} + m_{3} + m_{4}$와 같습니다. 저희는 여기서 '질량 함수' $p(x_{j})=m_{j}$를 정의할 수 있습니다. 따라서 전체 질량을 질량 함수를 통해 표기하면 $p(x_{1})+p(x_{2})+p(x_{3})+p(x_{4})$입니다.
이제 아래의 그림과 같이 L (m)의 통나무가 있고 $f(x)$의 밀도를 가지고 있다고 하겠습니다. 여기서 $f(x)$의 단위는 물리 법칙에 따라서 $\frac{질량}{길이}$입니다. 즉, 1m 당 f(x)의 질량을 가지는 것이죠.

기본적인 물리를 알고 계신다면 작은 범위의 질량은 $f(x_{i})\Delta x$임을 알고 계실껍니다. 만약 밀도($f(x)$)가 연속적으로 배정되어 있다면 저희는 통나무의 전체 질량을 적분을 통해 얻을 수 있습니다.
$$total\ mass=\int_{0}^{L} f(x) \; dx$$
제가 처음에 미적분학에 대해서 간단하게 설명한게 기억에 나실지 모르겠습니다. 기본적으로 적분=합이라고 언급하였습니다. 위의 적분식을 다시 표현하면
$$total\ mass \approx \sum_{i=1}^{n} f(x_{i})\Delta x$$
입니다. 해석하면 통나무를 굉장히 잘게 쪼갠다음 각 조각에 대한 질량을 전부 더한것입니다. 여기서 $\Delta x$를 무한히 작게 만들면 합에서 적분으로 바뀌게 되는 것이죠. 여기에 pdf는 완전히 동일합니다. 다른 점은 $f(x)$의 단위가 $\frac{probability}{unit x}$인 것이죠. 여기서 $x$의 단위는 매 번 다르기 때문에 특정할 수 없습니다. 또한 $f(x)dx$는 $\frac{probability}{unit x} \cdot (unit x)$이기 때문에 적분 결과가 확률이 될수 있습니다. 따라서 $f(1)$과 같은 값을 구할려고 한거라면 여러분은 특정 지점의 밀도를 구한것이지 질량, 즉 확률을 구한것이 아닙니다. 이제 본격적으로 직접 계산을 통해 연속확률변수의 확률을 계산해보겠습니다.
Ex1. $X$가 $[0, \frac{1}{3}]$pdf $f(x)=3$이라고 할 때(이 경우 나머지 범위에서는 $f(x)=0$이라는 의미입니다. 앞으로 이러한 표기 시 동일하게 적용하세요.), $P(0.1 \le X \le 0.2)$를 구하시오.
Answer
$P(0.1 \le X \le 0.2)=\int_{0.1}^{0.2} f(x) \; dx=\int_{0.1}^{0.2} 3 \; dx=\left. 3x \right|_{0.1}^{0.2}=0.3$
Ex2. $X$를 $[0, 1]$에서의 확률 변수이고 $f(x)=Cx_{2}$일 때, $C$의 값을 구하시오.
Answer
전체 확률은 1이 되어야하기 때문에 $1=\int_{-\infty}^{\infty} f(x) \; dx=\int_{0}^{1} Cx_{2}=\left. \frac{1}{3}Cx^{3} \right|_{0}^{1}=\frac{C}{3}$입니다. 따라서 $C=3$입니다.
다음 절로 넘어가기 전에 생각해보아야할게 있습니다. $X$가 연속확률변수일 때, $P(X=a)$이란 무엇일까요? $X$가 정확하게 $a$가 된다라는 것인데 연속확률변수 중에서 정확하게 특정 값이 될 수 있을 까요? 예를 들어 시간을 생각해보겠습니다. 소수점이 3개를 지원하는 디지털 시계로 시간을 잴 때 정확하게 10초가 될 때 정지를 누릅니다. 아마 여러분은 정말 많은 시도 끝에 운이 좋게 성공했습니다!! 그렇다면 소수점이 1000개를 지원하는 디지털 시계로 시간을 잴 때 정확하게 10초를 잴 수 있을 까요? 정말 힘들껍니다. 그리고 어째서 소수점이 유한하죠? 시간이 무한소수일 수도 있지 않겠습니까? 이 경우에는 정말 힘들껍니다. 따라서 연속확률변수에서 정확하게 특정 값이 되는 확률은 0입니다. 그렇다고 해서 그 값이 절대 발생하지않는 것은 아닙니다. 누군가 우주가 끝날 때까지 계속 반복한다면 가능성은 있습니다!
그래서 이산확률변수와는 다르게 연속확률변수에서는 확률 변수를 범위로 주게 됩니다!!
2.2. 누적확률분포(Cumulative Distribution Function; cdf)
연속확률변수의 누적확률분포는 이산확률변수와 완전히 똑같습니다!!
-누적확률분포 : $F(b)=P(X \le b)=\int_{-\infty}^{b} f(x) \; dx$
Ex3. Ex1의 cdf를 구하시오.
Answer
$a \in [0, \frac{1}{3}]$에 대해서 $F(a)=P(X \le a)=\int_{0}^{a} 3 \; dx=\left. 3x \right|_{0}^{a}=3a$입니다. 이를 함수로 표현하면
$$ f(x) = \left\{ \begin{array}{ll} 0 & \quad a < 0 \\ 3a & \quad 0 \le a \le \frac{1}{3} \\ 1 & \quad a > \frac{1}{3} \end{array} \right. $$
입니다. 이를 그림으로 그려보겠습니다.
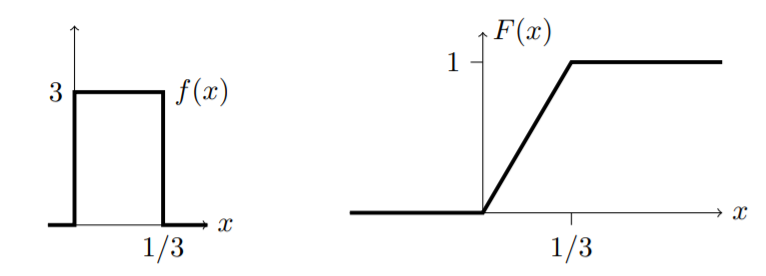
Ex4. Ex2의 cdf를 구하시오.
Answer
Ex2의 결과로 저희는 $C=3$이라는 것을 알았습니다. 즉, $x \in [0, 1]$에 대해서 $f(x)=3x^{2}$이죠. 이 pdf의 cdf는 $a \in [0, 1]$에 대해서 $F(a)=P(X \le a)=\int_{0}^{a} 3x^{2}=\left. x^{3} \right|_{0}^{a}=a^{3}$입니다.
$$ f(x) = \left\{ \begin{array}{ll} 0 & \quad a < 0 \\ a^{3} & \quad 0 \le a \le 1 \\ 1 & \quad a > 1 \end{array} \right. $$
이를 그림으로 그리면
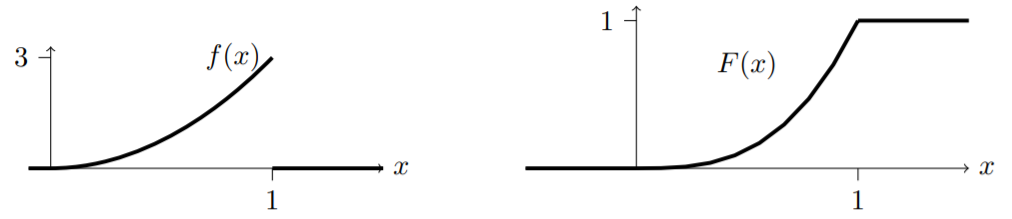
2.3. 누적확률분포의 성질
이산확률변수와는 다르게 연속확률변수의 누적확률분포의 성질은 적분이 들어가기 때문에 더 많습니다. 하지만 간단합니다.
-
정의 : $F(x)=P(X \le x)$
-
$0 \le F(x) \le 1$
-
$F(x)$는 감소하지 않는 함수입니다. 즉 $a \le b$라면 $F(a) \le F(b)$입니다.
-
$lim_{x \to \infty}F(x)=1$, $lim_{x \to -\infty}F(x)=0$
-
$P(a \le X \le b)=F(b)-F(a)$
-
$F^{'}(x)=f(x)$
1은 정의, 2, 3, 4는 이산확률변수에서 보던 성질과 동일합니다. 5의 경우 간단한 계산을 통해 유도가능합니다.
$$\int_{-\infty}^{b} f(x) \; dx=\int_{-\infty}^{a} f(x) \; dx +\int_{a}^{b} f(x) \; dx$$
$$\int_{a}^{b} f(x) \; dx=\int_{-\infty}^{b} f(x) \; dx-\int_{-\infty}^{a} f(x) \; dx$$
$$P(a \le X \le b)=F(b)-F(a)$$
6은 미적분학의 기본정리(Fundamental theorem of calculas)입니다.
기초통계학[8].연속확률변수의 분포(https://everyday-image-processing.tistory.com/14)
'수학 > 기초통계학' 카테고리의 다른 글
| 기초통계학[9].연속확률변수의 조작 (0) | 2020.03.16 |
|---|---|
| 기초통계학[8].연속확률변수의 분포 (1) | 2020.03.16 |
| 기초통계학[6].이산확률변수의 분산 (0) | 2020.03.13 |
| 기초통계학[5]. 이산확률변수의 기댓값 (0) | 2020.03.12 |
| 기초통계학[4].이산확률변수 (0) | 2020.03.08 |
안녕하세요. 오늘은 지난 시간의 기초통계학[6].이산확률변수의 분산(https://everyday-image-processing.tistory.com/11)에 이어서 연속확률변수에 대해 알아보겠습니다.
1. 미적분학
이제 이산확률변수가 아닌 연속확률변수로 주제가 바뀌었습니다. 이산확률변수에서 확률을 계산하기 위해 ∑을 사용했다면 연속확률변수에서는 확률을 계산하려면 ∫을 사용합니다. 따라서 본격적으로 연속확률변수에 대해서 알아보기전에 간단한 미적분학 개념을 설명하겠습니다.(이후에 시간이 된다면 미적분학을 포스팅하겠습니다.) 참고로 고등학교 때 배우는 이과 미적분학으로도 충분합니다.(제가 고등학교다닐 때는 문이과가 나뉘어져있었는데 최근에는 문이과 통합이라고 들었습니다...)
기본적으로 어떤 함수를 적분한다는 것은 함수의 밑부분의 넓이를 구한다라는 말입니다. 따라서, ∫baf(x)dx는 y=f(x)의 [a,b]구간의 밑부분의 넓이(=area)와 같습니다.
또한 개념적으로 적분은 합(∑)과 같습니다. 그러므로 ∫baf(x)dx는 f(x)dx의 합과 같습니다.
위 두 개념을 하나로 합치면 area≈sum of retangle areas=f(x1)Δx+f(x2)Δx+⋯+f(xn)Δx=∑ni=1f(xi)Δ입니다. 이를 도식화하면 아래의 그림과 같습니다.
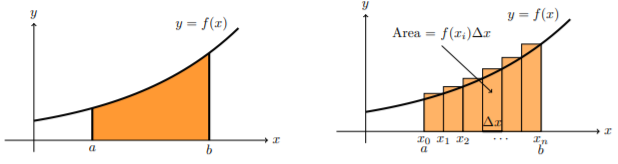
이제 Δx를 굉장히 작게 줄이면 오른쪽 영역은 왼쪽 영역과 거의 비슷하고 언젠가는 차이가 0에 가까워질것입니다. (미적분학에서는 이런 무한, 극한의 개념을 이해하는 것이 중요합니다.)
2. 연속확률변수(Continuous Random Variables)과 확률 밀도 함수(Probability Density Functions; pdf)
연속확률변수는 이산확률변수와 다르게 범위로 주어집니다. 이 범위는 일반적으로 [0,1], (0,∞)와 같이 무한한 원소를 포함합니다. 그 이유는 잠시 뒤에 소개됩니다.
-연속확률변수 : c≤d를 만족하는 상수 c, d에 대해서 P(c≤X≤d)=∫dcf(x)dx인 f(x)가 존재한다면 확률 변수 X는 연속확률변수라고 합니다. 또한 이러한 f(x)는 확률 밀도 함수(pdf)라고 합니다. 이때, 확률 밀도 함수는 1. f(x)≥0, 2. ∫∞−∞f(x)dx=1를 만족해야합니다.
저희가 이전에 이산확률변수의 확률 질량 함수(p(x))를 다루었던 것과 같이 거의 비슷하지만 가장 큰 차이점이 있습니다. 먼저, p(x)와는 다르게 f(x)는 확률을 의미하지 않습니다. 연속확률변수에서의 확률은 f(x)의 특정 범위를 적분해야 얻을 수 있습니다. f(x)가 확률이 아니기 때문에 f(x)가 반드시 1보다 작거나 같아야한다는 제약조건은 없어지게 됩니다.
연속확률변수에서의 확률을 그림으로 표현하면 아래와 같습니다.

이때, P(c≤X≤d)는 초록색 그래프에서 [c,d] 범위 내의 밑부분의 넓이를 의미합니다.
2.1. 확률 질량과 확률 밀도
이산확률변수에서도 뜬금없이 질량이라는 단어가 언급되었습니다. 이전에는 통계에서 질량은 확률이라고 했습니다. 이번에는 밀도라는 단어가 언급되었군요. 어째서 pmf를 설명할 때는 질량, pdf를 설명할 때는 밀도라는 단어를 사용하는 것일까요? 일단 여기서 쓰이는 질량과 밀도는 기본적으로 물리에서 보는 질량과 밀도의 정의와 완벽하게 일치한다는 점에 유의해주시길 바랍니다.
먼저 질량에 대해서 설명하자면 아래의 그림과 같이 질량이 m1,m2,m3,m4인 물체가 있다고 가정하겠습니다.

그렇다면 전체 질량은 m1+m2+m3+m4와 같습니다. 저희는 여기서 '질량 함수' p(xj)=mj를 정의할 수 있습니다. 따라서 전체 질량을 질량 함수를 통해 표기하면 p(x1)+p(x2)+p(x3)+p(x4)입니다.
이제 아래의 그림과 같이 L (m)의 통나무가 있고 f(x)의 밀도를 가지고 있다고 하겠습니다. 여기서 f(x)의 단위는 물리 법칙에 따라서 질량길이입니다. 즉, 1m 당 f(x)의 질량을 가지는 것이죠.

기본적인 물리를 알고 계신다면 작은 범위의 질량은 f(xi)Δx임을 알고 계실껍니다. 만약 밀도(f(x))가 연속적으로 배정되어 있다면 저희는 통나무의 전체 질량을 적분을 통해 얻을 수 있습니다.
total mass=∫L0f(x)dx
제가 처음에 미적분학에 대해서 간단하게 설명한게 기억에 나실지 모르겠습니다. 기본적으로 적분=합이라고 언급하였습니다. 위의 적분식을 다시 표현하면
total mass≈n∑i=1f(xi)Δx
입니다. 해석하면 통나무를 굉장히 잘게 쪼갠다음 각 조각에 대한 질량을 전부 더한것입니다. 여기서 Δx를 무한히 작게 만들면 합에서 적분으로 바뀌게 되는 것이죠. 여기에 pdf는 완전히 동일합니다. 다른 점은 f(x)의 단위가 probabilityunitx인 것이죠. 여기서 x의 단위는 매 번 다르기 때문에 특정할 수 없습니다. 또한 f(x)dx는 probabilityunitx⋅(unitx)이기 때문에 적분 결과가 확률이 될수 있습니다. 따라서 f(1)과 같은 값을 구할려고 한거라면 여러분은 특정 지점의 밀도를 구한것이지 질량, 즉 확률을 구한것이 아닙니다. 이제 본격적으로 직접 계산을 통해 연속확률변수의 확률을 계산해보겠습니다.
Ex1. X가 [0,13]pdf f(x)=3이라고 할 때(이 경우 나머지 범위에서는 f(x)=0이라는 의미입니다. 앞으로 이러한 표기 시 동일하게 적용하세요.), P(0.1≤X≤0.2)를 구하시오.
Answer
P(0.1≤X≤0.2)=∫0.20.1f(x)dx=∫0.20.13dx=3x|0.20.1=0.3
Ex2. X를 [0,1]에서의 확률 변수이고 f(x)=Cx2일 때, C의 값을 구하시오.
Answer
전체 확률은 1이 되어야하기 때문에 1=∫∞−∞f(x)dx=∫10Cx2=13Cx3|10=C3입니다. 따라서 C=3입니다.
다음 절로 넘어가기 전에 생각해보아야할게 있습니다. X가 연속확률변수일 때, P(X=a)이란 무엇일까요? X가 정확하게 a가 된다라는 것인데 연속확률변수 중에서 정확하게 특정 값이 될 수 있을 까요? 예를 들어 시간을 생각해보겠습니다. 소수점이 3개를 지원하는 디지털 시계로 시간을 잴 때 정확하게 10초가 될 때 정지를 누릅니다. 아마 여러분은 정말 많은 시도 끝에 운이 좋게 성공했습니다!! 그렇다면 소수점이 1000개를 지원하는 디지털 시계로 시간을 잴 때 정확하게 10초를 잴 수 있을 까요? 정말 힘들껍니다. 그리고 어째서 소수점이 유한하죠? 시간이 무한소수일 수도 있지 않겠습니까? 이 경우에는 정말 힘들껍니다. 따라서 연속확률변수에서 정확하게 특정 값이 되는 확률은 0입니다. 그렇다고 해서 그 값이 절대 발생하지않는 것은 아닙니다. 누군가 우주가 끝날 때까지 계속 반복한다면 가능성은 있습니다!
그래서 이산확률변수와는 다르게 연속확률변수에서는 확률 변수를 범위로 주게 됩니다!!
2.2. 누적확률분포(Cumulative Distribution Function; cdf)
연속확률변수의 누적확률분포는 이산확률변수와 완전히 똑같습니다!!
-누적확률분포 : F(b)=P(X≤b)=∫b−∞f(x)dx
Ex3. Ex1의 cdf를 구하시오.
Answer
a∈[0,13]에 대해서 F(a)=P(X≤a)=∫a03dx=3x|a0=3a입니다. 이를 함수로 표현하면
f(x)={0a<03a0≤a≤131a>13
입니다. 이를 그림으로 그려보겠습니다.

Ex4. Ex2의 cdf를 구하시오.
Answer
Ex2의 결과로 저희는 C=3이라는 것을 알았습니다. 즉, x∈[0,1]에 대해서 f(x)=3x2이죠. 이 pdf의 cdf는 a∈[0,1]에 대해서 F(a)=P(X≤a)=∫a03x2=x3|a0=a3입니다.
f(x)={0a<0a30≤a≤11a>1
이를 그림으로 그리면

2.3. 누적확률분포의 성질
이산확률변수와는 다르게 연속확률변수의 누적확률분포의 성질은 적분이 들어가기 때문에 더 많습니다. 하지만 간단합니다.
-
정의 : F(x)=P(X≤x)
-
0≤F(x)≤1
-
F(x)는 감소하지 않는 함수입니다. 즉 a≤b라면 F(a)≤F(b)입니다.
-
limx→∞F(x)=1, limx→−∞F(x)=0
-
P(a≤X≤b)=F(b)−F(a)
-
F′(x)=f(x)
1은 정의, 2, 3, 4는 이산확률변수에서 보던 성질과 동일합니다. 5의 경우 간단한 계산을 통해 유도가능합니다.
∫b−∞f(x)dx=∫a−∞f(x)dx+∫baf(x)dx
∫baf(x)dx=∫b−∞f(x)dx−∫a−∞f(x)dx
P(a≤X≤b)=F(b)−F(a)
6은 미적분학의 기본정리(Fundamental theorem of calculas)입니다.
기초통계학[8].연속확률변수의 분포(https://everyday-image-processing.tistory.com/14)
'수학 > 기초통계학' 카테고리의 다른 글
| 기초통계학[9].연속확률변수의 조작 (0) | 2020.03.16 |
|---|---|
| 기초통계학[8].연속확률변수의 분포 (1) | 2020.03.16 |
| 기초통계학[6].이산확률변수의 분산 (0) | 2020.03.13 |
| 기초통계학[5]. 이산확률변수의 기댓값 (0) | 2020.03.12 |
| 기초통계학[4].이산확률변수 (0) | 2020.03.08 |
