안녕하세요. 지난 포스팅의 디지털 영상 처리 - 디지털 영상 기초 1에서는 디지털 영상을 이해하기 위한 배경 지식을 알아보았습니다. 오늘도 계속 이어서 진행해보도록 하겠습니다.
1. 디지털 영상 획득(digital image acquisition)
저희가 실제로 보는 영상을 디지털화하려면 어떻게 해야할까요? 이를 위해서는 영상이 무엇때문에 생기는 것인지 알아봐야합니다. 다들 아시겠지만 저희가 영상을 인식하는 과정은 광원에서 시작된 빛이 물체에 반사되어 눈에 입력되어 원추세포와 간상세포가 입력된 빛에서 파장을 분석하여 이를 다시 뇌로 전송하게 됩니다. 즉, 어떤 영상을 인식하기 위해서는 "빛"과 "반사"은 필수요소가 됩니다. 둘 중 하나라도 없으면 저희가 영상을 인식하는 것을 불가능해지죠. 이는 다른 영상을 얻는 다양한 장치들에서도 마찬가지로 적용됩니다.
하지만, 오직 가시광선만 인식할 수 있는 사람과는 다르게 장치는 다양한 광원들을 활용할 수 있습니다. 대표적으로 X선 이용한 투시 장비는 신체 내부의 골격구조를 보거나 공항 검색대, 또한 공장에서 이상물질 검출과 같은 다양한 분야에서 사용되고 있습니다. 그렇다면 특정 광원을 통해서 물체에 반사된 광원을 인식하려면 어떻게 해야할까요? 이를 위한 장치는 크게 3가지로 나뉩니다.
1.1. 단일 센서(single sensor)
가장 단순한 방법은 하나의 장치가 하나의 광원을 인식하는 방법입니다. 이를 대표하는 장치가 바로 광다이오드(photodiode; 포토다이오드)라고 합니다. 광다이오드에는 소자에 민감한 부분에 빛이 들어오도록 창이나 광섬유 연결패키지가 있습니다. 어떤 광다이오드는 창없이 X선이나 자외선을 검출하기도 한답니다.
하지만, 저희는 "영상"을 검출하고 싶습니다. 따라서 $x$ 방향과 $y$ 방향의 변위에 의존할 수 밖에 없는 데요. 이를 해결하기 위해서 아래의 그림과 같이 1개의 센서가 원통이 돌면서 인식하게 됩니다.
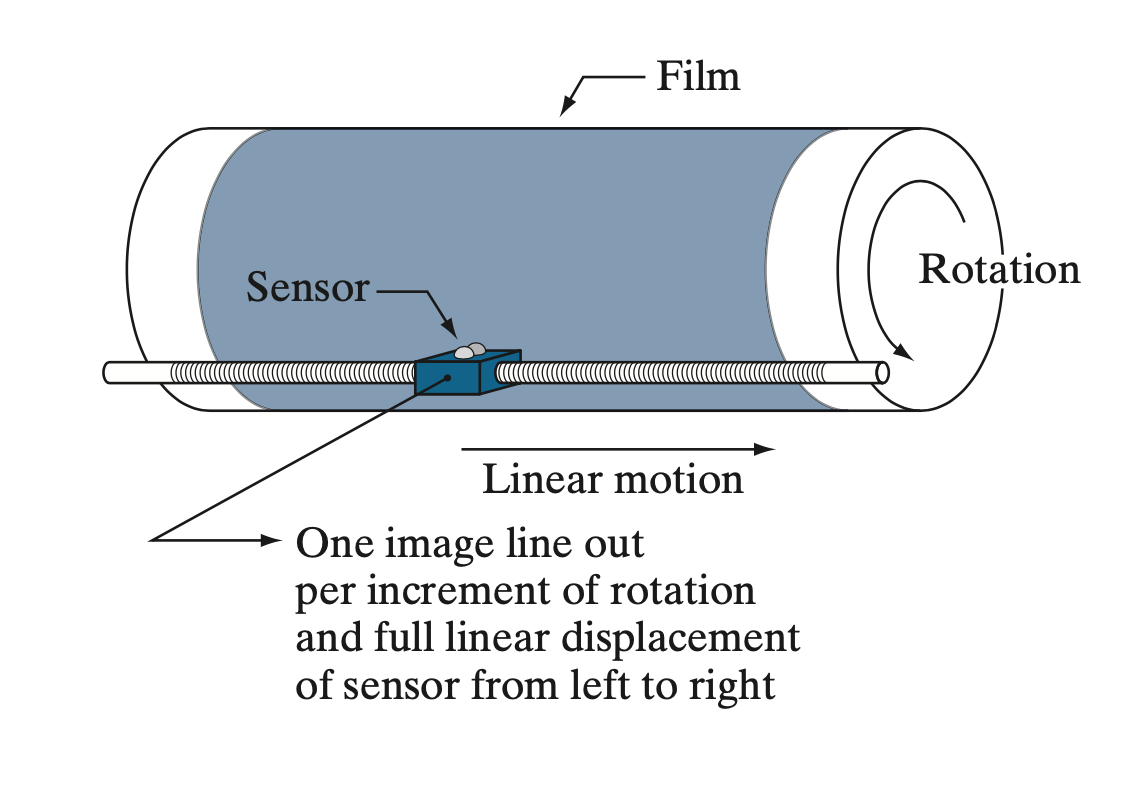
이 방법은 기본적으로 1개의 센서만을 이용하기 때문에 가장 싼 방법입니다. 그리고 생각보다 높은 해상도의 결과를 얻을 수 있죠. 하지만! 아무래도 1개의 센서를 이용하다보니 영상을 얻는 속도가 느릴 수 밖에 없는 것은 단점입니다.
1.2. 스트립 센서(strip sensor)
단일 센서의 단점은 1개의 센서를 이용하기 때문에 속도가 느립니다. 따라서 이를 보완하기 위해서 여러 개의 센서를 일렬로 나열한 스트립 센서가 개발됩니다. 이러한 센서 형태는 아래의 그림과 같이 플랫 베드 형태에 많이 쓰입니다. 대표적으로 MRI, CT 등이 있겠죠?

1.3. 배열 센서(array sensor)
배열 센서는 주로 카메라의 CCD(Charge-Coupled Device)를 구성할 때 사용되는 구조입니다. 스마트폰과 같은 소형 카메라에는 가로, 세로 각각 4000개 씩의 센서가 자리잡고 있습니다. 각 센서는 초록색, 빨간색, 파란색"만" 인식합니다. 이는 이때 초록색의 비율이 가장 많은 데, 그 이유는 사람이 초록색에 더 민감하게 반응하기 때문에 더 섬세한 표현을 위해 초록색 센서를 더 많이 추가한 것입니다.
1.4. 디지털 영상의 공식화
지난 포스팅에서도 미리 설명드렸지만 디지털 영상 처리는 수학적 배경이 많이 필요합니다. 따라서 디지털 영상을 수학적으로 처리할 수 있는 도구가 필요하다는 것이죠. 이번 절에서는 그에 대한 내용을 해보고자 합니다.

물체에 반사된 광원이 이미징 센서가 검출하게 되면 image plane과 같이 일단 내부적으로 이미징 센서 방향에서 바라봤을 때의 장면을 얻을 수 있습니다. 하지만, 저희는 컴퓨터에서 정보를 처리해야하기 때문에 연속적인 데이터를 가지는 image plane을 그대로 사용할 수 없고 "양자화(quatization)"이라는 과정을 통해 영상을 이산적으로 얻습니다. 이렇게 얻은 결과를 $f(x, y)$라고 정의하겠습니다. 여기서 디지털 영상이 되려면 모든 $(x, y)$에 대해서 $0 \le f(x, y) < \infty$가 되어야합니다.
여기서 위의 그림을 보면 $f(x, y)$는 물체로부터 반사된 광원과 오리지널 광원에 동시에 영향을 받고 있음을 볼 수 있습니다. 이를 각각 $r(x, y), i(x, y)$라고 정의하겠습니다. 그러면 저희는 $f(x, y) = i(x, y) \cdot r(x, y)$와 같이 쓸 수 있으며 이때, $0 \le i(x, y) < \infty$, 그리고 $0 \le r(x, y) \le 1$로 제한됩니다. 여기서 $r(x, y) = 0$이면 물체가 완전히 광원을 흡수하여 반사하는 빛이 없다는 것을 의미합니다. 그리고 $r(x, y) = 1$이면 물체가 완전히 광원을 반사하였다는 의미로 받아들이시면 됩니다.
2. 영상 샘플링과 양자화
이제 어떤 과정을 통해서 영상을 얻었다고 가정하겠습니다. 그러면 자연영상은 연속된 값(1.45, 56.23, ... 등등)으로 이루어지기 때문에 이산 데이터를 처리하는 컴퓨터에서 영상을 처리하기 위해서는 디지털 형태로 변화해주는 과정이 필요합니다. 이 과정은 2가지의 스텝으로 이루어지는 데, 이를 각각 샘플링(sampling)과 양자화(quantization)이라고 합니다. 먼저, 자연 영상은 특정 영역을 디지털 형태로 변환한다고 가정하겠습니다. 그러면 아래 그림과 같이 특정 영역에 대한 자연 데이터를 얻을 수 있습니다.

그 다음으로 추출된 자연 데이터에서 특정 간격만큼 샘플링과 양자화를 하게 됩니다. 간단하게 표현하면 샘플링은 $x$축에 대해서 적용하고, 양자화는 $y$축에 대해서 적용하는 것입니다. 이를 아래의 그림과 같이 표현할 수 있습니다.

이 과정을 모든 영역에 대해서 적용하면 아래의 결과를 얻게 됩니다.

이를 수학적으로 간단하게 표현할 수 있습니다. 두 개의 연속 변수 $s, t$의 함수 $f(s, t)$는 위의 샘플링과 양자화 과정으로 인해서 두 개의 이산 변수인 $x = 0, 1, \dots, M-1$, 그리고 $y = 0, 1, \dots, N-1$의 조합 $(x, y)$의 음이 아닌 값을 가지는 함수 $f(x, y) \in \mathbb{R}^{M \times N}$으로 표현할 수 있습니다. 결과적으로 디지털 영상은 2차원 데이터로써 아래와 같은 행렬로 표현할 수 있다는 것을 볼 수 있습니다.
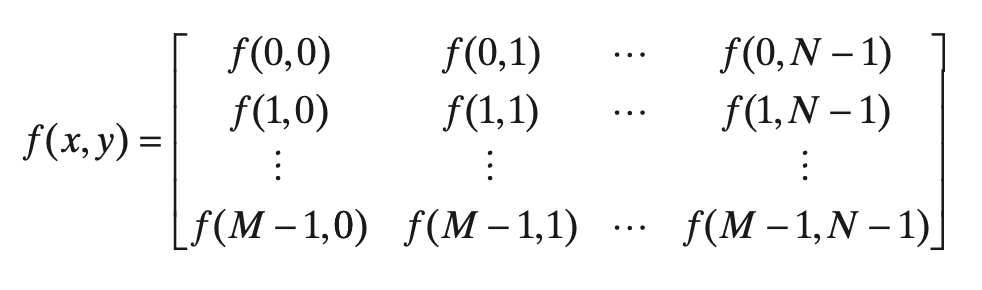
물론 아래와 같이 함수적인 표현이 아닌 아래와 같이 선형대수학에 중점을 둔 변환 행렬로써 적을 수도 있습니다.

3. 픽셀 관계
가장 처음에 디지털 영상의 각 요소는 픽셀이라는 단위로 구성된 2차원 이상의 데이터라고 표현하였습니다. 따라서 픽셀은 샘플링을 통해 얻은 좌표값에 대한 데이터 $p = f(x, y)$라고 표현할 수 있습니다. 여기서 저희가 추가적으로 고려할 것은 픽셀간의 관계성입니다. 이를 통해서 나중에 알아볼 객체 분할과 같은 분야에 쓰일 수 있습니다. 용어를 중심으로 알아보도록 하겠습니다.
가장 간단한 관계는 임의의 $(x, y)$ 좌표에 대응되는 값에 대해서 하나의 모서리를 공유하는 픽셀들일 것입니다. 이를 픽셀 $p$의 4-이웃(4-neighborhoods of $p$), $N_{4}(p)$라고 말합니다. 유사한 관계로는 대각선 이웃들만 고려하는 방법도 있습니다. 이를 $N_{D}(p)$라고 말합니다. 마지막으로 $N_{8}(p)$는 $N_{D}(p)$와 $N_{4}(p)$를 함께 고려하여 표현하면 $N_{8}(p) = N_{4}(p) \cup N_{D}(p)$가 됩니다. 이를 그림으로 보시면 더욱 명확해지실 겁니다.
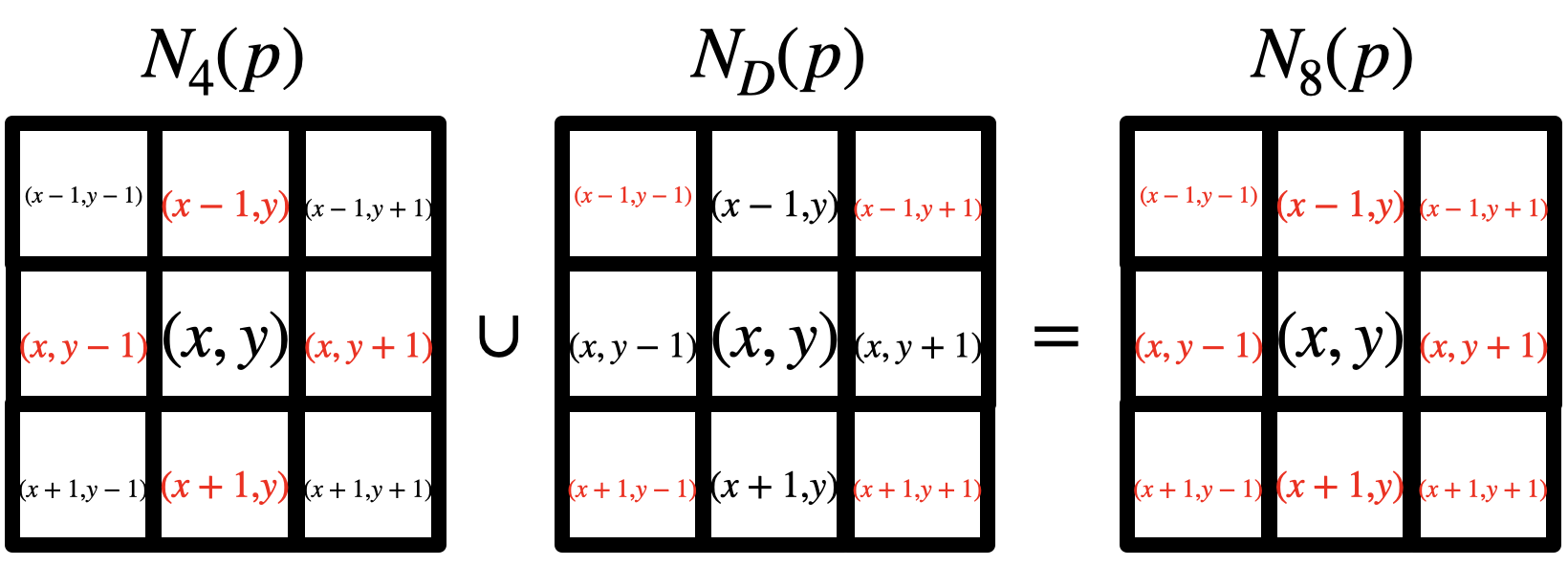
이를 정리하면 임의의 픽셀 $(x, y)$에 대해서 3가지 종류의 이웃을 정의하면
- $N_{4}(p) = \{(x - 1, y), (x, y + 1), (x + 1, y), (x, y - 1)\}$
- $N_{D}(p) = \{(x - 1, y - 1), (x - 1, y + 1), (x + 1, y + 1), (x + 1, y - 1)\}$
- $N_{8}(p) = N_{4}(p) \cup N_{D}(p) = \{(x - 1, y - 1), (x - 1, y), (x - 1, y + 1), (x, y + 1), (x + 1, y + 1), (x + 1, y), (x + 1, y - 1), (x, y - 1)\}$
1). 인접성(adjacency)
인접성을 정의하기 위해서 집합 $V$를 밝기값의 집합이라고 정의하겠습니다. 이때, 바이너리 영상이라고 가정하면 가능한 밝기값이 0 또는 1입니다. 이때, 해당 영상에 0만 들어가 있다면 $V =\{0\}$, 1만 들어가 있다면 $V = \{1\}$, 0과 1이 같이 있다면 $V = \{0, 1\}$이라고 적을 수 있으며, 이를 확장하여 그레이 스케일 영상에도 적용할 수 있습니다. 이를 통해서 3가지 종류의 인접성을 정의할 수 있습니다.
- 4-인접성(4-adjacency) : 밝기 집합 $V$로부터의 밝기를 가지는 2개의 픽셀 $p$와 $q$에 대해서 $q \in N_{4}(p)$인 경우
- 8-인접성(8-adjacency) : 밝기 집합 $V$로부터의 밝기를 가지는 2개의 픽셀 $p$와 $q$에 대해서 $q \in N_{8}(p)$인 경우
- m-인접성(m-adjacency), 또는 혼잡-인접성(mixed-adjacency) : 밝기 집합 $V$로부터 밝기를 가지는 2개의 픽셀 $p$와 $q$에 대해서 $q \in N_{4}(p)$이거나 $q \in N_{D}(p)$ 이고 $N_{4}(p) \cap N_{4}(q) = \emptyset$인 경우
말로는 어려우니 그림을 통해서 보도록 하겠습니다. 문제를 단순화하기 위해서 여기서는 바이너리 영상, 그리고 $V = \{1\}$이라고 가정하도록 하겠습니다.
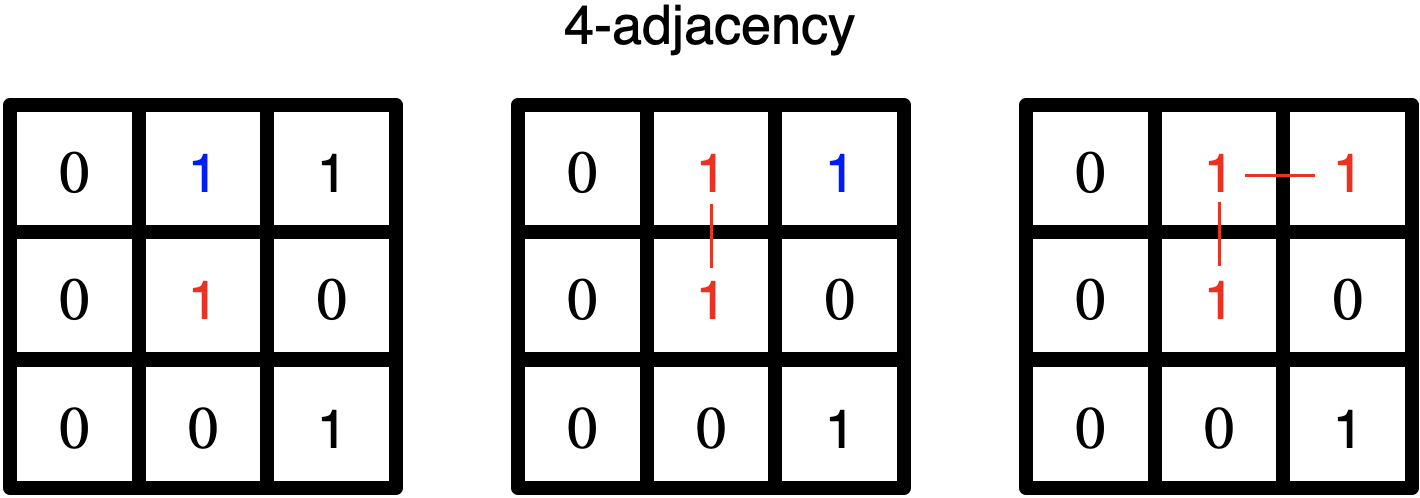
먼저, 4-인접성부터 확인해보면 가장 왼쪽의 경우 가장 가운데 픽셀부터 시작하여 $N_{4}(p)$에 해당하는 픽셀들이면서 픽셀값이 1인 픽셀들을 찾아야합니다. 그에 해당하는 픽셀이 바로 가운데 픽셀을 기준으로 바로 위에 있는 픽셀이죠. 이 둘을 연결해줍니다. 그러면 가운데 그림과 같이 $(x, y), (x - 1, y)$가 서로 연결되게 됩니다. 이제 새로운 픽셀 $(x - 1, y)$을 기준으로 처음에 했던 과정을 한번 더 수행합니다. 그러면 $(x - 1, y + 1)$에 해당하는 픽셀이 조건에 부합한다는 것을 볼 수 있습니다. 따라서 오른쪽 그림과 같이 연결해주게 됩니다. 그러면 더이상 연결할 픽셀이 없기 때문에 이것이 최종 결과가 되는 것입니다.

그 다음으로 8-인접성은 4-인접성보다 더 많은 픽셀을 확인해야하기 때문에 과정이 더 길어졌습니다. 하지만, 큰 틀은 4-인접성을 벗어나지 않았기 때문에 간단합니다. 4-인접성과 마찬가지로 가장 먼저 $(x, y)$ 픽셀을 기준으로 확인해보면 $N_{8}(p)$에 해당하면서 픽셀값이 1인 픽셀들을 찾습니다. 그러면 총 3개의 픽셀 $(x - 1, y), (x - 1, y + 1), (x + 1, y + 1)$이 그 조건을 만족하게 됩니다. 그러면 2번째 그림부터 4번째 그림까지는 해당 픽셀들을 연결하는 과정을 그린 것입니다.
이제 추가된 픽셀들에 대해서도 조건을 만족하는 인접 픽셀들을 찾아야하는 데 $(x - 1, y)$를 보면 8-인접성에 만족하는 픽셀 $(x - 1, y + 1)$ 하나가 아직 연결되지 않은 채로 존재하고 있기 때문에 마지막으로 두 픽셀 사이를 이어주면 최종적으로 8-인접성을 얻을 수 있습니다.

마지막으로 혼합-인접성입니다. 혼합 인접성은 4-인접성이나 8-인접성에 비해 더 강력한 조건을 가지고 있다는 것을 볼 수 있습니다. 조건을 자세히 보시면 이웃 픽셀에 포함된다고 항상 인접성 픽셀에 포함되지 않고 있습니다. 4-인접성이나 8-인접성과 마찬가지로 가장 먼저 $(x, y)$ 픽셀을 기준으로 확인해보면 1번 조건은 처음에 설명한 4-인접성과 그냥 동일합니다. 따라서 $(x - 1, y)$ 픽셀을 첫번째 조건에 부합하기 때문에 혼합-인접성에 추가합니다. 2번 조건은 $N_{D}((x, y))$를 고려합니다.
그러면 $(x - 1, y + 1), (x + 1, y + 1)$를 확인하면 됩니다. 하지만, $(x - 1, y + 1)$의 경우에는 3번 조건에 부합하지 않습니다. 왜냐하면, $N_{4}((x, y)) = \{(x - 1, y)\}$이고 $N_{4}((x - 1, y + 1)) = \{(x - 1, y)\}$로 $N_{4}((x, y)) \cap N_{4}((x - 1, y + 1)) \neq \emptyset$이기 때문입니다. 따라서 두 픽셀은 연결되지 않습니다.
이제 다음 후보 픽셀인 $(x + 1, y + 1)$을 확인해보면 $N_{4}((x + 1, y + 1)) \cap N_{4}((x , y)) = \emptyset$이기 때문에 두 픽셀이 연결될 수 있습니다. 이 과정에서 새롭게 추가된 픽셀을 $(x - 1, y)$와 $(x + 1, y + 1)$입니다. 이제 $(x - 1, y)$ 픽셀을 기준으로 확인해보면 4-인접성에 해당하는 픽셀이 $(x - 1, y + 1)$이 있기 때문에 두 픽셀을 연결합니다. 하지만, $(x + 1, y + 1)$은 1번 조건을 만족하지 않아서 2번 조건을 확인해야 하지만 이기 두 픽셀이 연결되어 있기 때문에 넘어갑니다.
마지막으로 새로 추가된 $(x - 1, y + 1)$ 픽셀의 경우에 2번 조건을 만족하는 픽셀은 있으나 3번 조건을 만족하지 않아 두 픽셀이 연결되지 않는다는 것을 볼 수 있습니다. 이 과정으로 가장 오른쪽 그림과 같은 혼합-인접성을 얻을 수 있습니다.
이를 하나의 그림으로 정리해보면 아래와 같습니다. 동일한 데이터라고 하더라도 어떤 인접성이냐에 따라서 연결되는 픽셀들이 달라지는 것을 관찰할 수 있습니다.

그렇다면 왜 혼합-인접성이 도입된 것 일까요? 일단 기본적으로 혼합-인접성의 정의를 보면 $N_{4}(p)$와 $N_{D}(p)$를 동시에 고려한다는 점에서 8-인접성과 어떻게 보면 유사한 결과를 얻었다고 볼 수 있습니다. 실제로 1개의 경로를 제외하고는 두 인접성은 동일합니다. 하지만, 8-인접성에는 큰 문제가 존재합니다. 바로 "모호성(ambiguous)"이 존재합니다. 즉, 픽셀에서 픽셀로의 경로가 1개가 아니라는 점입니다. 위의 예제에서 $(x, y) \rightarrow (x - 1, y + 1)$로의 경로를 확인해보면 8-인접성에는 2개의 경로가 존재한다는 점에서 이를 모호성이락고 표현합니다. 하지만 혼합-인접성은 이러한 모호성을 없애기 위해서 도입하였기 때문에 경로가 유일한 것을 볼 수 있습니다.
2). 디지털 경로(digital path)
디지털 경로는 시작 픽셀 $(x, y)$로부터 목적 픽셀 $(s, t)$까지 도달하는 데 필요한 서로 다른 인접 픽셀 $(x_{i}, y_{i})$의 순서라고 정의할 수 있습니다.
$$(x_{0}, y_{0}), (x_{1}, y_{1}), \dots, (x_{n}, y_{n})$$
이때, 시작 픽셀은 $(x, y) = (x_{0}, y_{0})$이고 목적 픽셀은 $(s, t) = (x_{n}, y_{n})$이 됩니다. 여기서 어떤 인접성을 사용하느냐에 따라서 분류가 되는 데 4-, 8-, 혼합-인접성에 따라서 각각 4-경로, 8-경로, 혼합-경로(m-경로)라고 정의됩니다.
3). 연결성(connectiveness)
집합 $S$를 영상 픽셀의 부분 집합이라고 정의했을 때, 만약 $S$안의 픽셀 $p, q$ 사이에 경로가 존재한다면 두 픽셀에는 연결성(connected)이 존재한다고 정의합니다. 만약, 집합 $S$에서 어떠한 픽셀 $p$를 가져오더라도 집합 $S$ 내에서 $p$를 제외한 다른 픽셀들 사이에 전부 연결성이 존재한다면 연결된 픽셀들을 하나의 집합 $T$로 묶어서 집합 $T$를 연결 요소(connected component)라고 정의합니다. 만약, 그 연결 요소의 원소가 유일하다면 그 연결 요소를 포함하고 있는 집합 $S$는 연결 집합(connected set)이라고 정의합니다. 예를 들어서 설명하면 이전에 인접성을 설명할 때, 모든 요소가 서로 연결되어 있으며 연결간에 유일하게 경로가 존재합니다. 따라서 해당 영상을 연결 집합이라고 정의할 수 있습니다. 하지만, 8-인접성은 픽셀간의 경로가 유일하지 않기 때문에 연결 집합이라고 부를 수 없습니다.
4). 영역(region)
집합 $R$을 영상의 부분 집합이라고 가정하겠습니다. 만약, 집합 $R$이 연결 집합이라면 집합 $R$을 조금 더 영상 처리다운 용어로서 영역(region)이라는 것으로 정의합니다. 저희가 인접성에 대해서 정의할 때는 픽셀간의 인접성을 정의하였습니다. 하지만 이를 확장하여 영역 간의 인접성도 정의해볼 수 있습니다. 두 개의 영역 $R_{i}, R_{j}$에 대해서 $R_{i} \cup R_{j}$가 연결 집합이라면 두 집합은 인접(adjacency)한다라고 정의합니다. 예를 들면 아래와 같은 그림이라고 볼 수 있겠습니다. 만약, 두 영역 사이에 인접성이 존재하지 않는 다면 두 영역이 서로소(disjoint)라고 정의합니다.

영역을 이용해서 "전경(forground)"와 "배경(background)"를 정의할 수 있습니다. 먼저, $K$개의 서로소 영역, $R_{1}, R_{2}, \dots, R_{K}$가 있다고 가정해겠습니다. 그리고 $R_{u} = \cup_{i=1}^{K} R_{i}$를 고려합니다. 즉, $R_{u}$는 $K$개의 모든 서로소 영역의 합집합이 됩니다. 여기서 $R_{u}, (R_{u})^{c}$를 각각 전경, 배경으로 정의합니다.
5). 거리 측정
마지막으로 알아볼 것은 두 개의 픽셀 사이의 거리(distance)를 측정하는 방법에 대해서 알아보겠습니다. 수학적으로 정의했을 때 어떤 함수 $D$가 "거리"라고 부르기 위해서는 아래의 3가지 조건을 만족해야합니다.
- $D(p, q) \ge 0$이고 $D(p, q) = 0$이면 $p = q$
- $D(p, q) = D(q, p)$
- $D(p, s) \le D(p, q) + D(q, s)$
특히, 마지막 조건은 삼각 부등식(triangular inequality)라고 불리는 아주 유명한 식입니다. 이때, 거리의 이름은 위의 조건을 만족함과 동시에 거리의 정의에 따라 달라집니다. 그 중 대표적인 3개의 거리 함수를 확인해보고 오늘은 여기까지 진행하도록 하겠습니다.
- $D_{e}(p, q) = \left[(x - u)^{2} + (y - t)^{2}\right]$
- $D_{4}(p, q) = \left|x - u\right| + \left|y - t\right|$
- $D_{8}(p, q) = \text{max}(\left|x - u\right|, \left|y - t\right|)$
'image processing' 카테고리의 다른 글
| 디지털 영상 처리 - 히스토그램 평활화(histogram equalization) (14) | 2021.02.12 |
|---|---|
| 디지털 영상 처리 - 영상 히스토그램(Image Histogram) (4) | 2021.02.02 |
| 디지털 영상 처리 - 밝기 변환 함수 (0) | 2021.01.20 |
| 디지털 영상 처리 - 디지털 영상 기초 1 (0) | 2021.01.08 |
| 디지털 영상 처리 - 소개 (0) | 2020.12.25 |
