저희는 이전 포스팅까지 빈도주의적 가설검정을 중심으로, 가능도비 검정과 제1·2종 오류 및 Neyman–Pearson 보조정리를 살펴보고, NHST와 p-값의 정의와 활용을 정리한 뒤, p-값이 자주 잘못 해석되며 실제로는 귀무가설 사후확률과 큰 차이가 날 수 있다는 문제를 다루었습니다. 이어서 왜 모두가 베이지안을 택하지 않는지에 대한 역사적 및 실무적 이유를 검토하였습니다. 결론적으로 원칙적으로는 베이지안 추론이 합리적이지만 실제 적용에서는 데이터와 상황에 맞게 보정된 절차를 병행하는 것이 바람직하다는 점을 확인하였습니다.
1. 엔트로피(Entropy)
이번 포스팅부터는 정보 이론 분야의 몇 가지 중요한 기본 개념을 소개하고자 합니다. 확률분포의 엔트로피(entropy)는 주어진 분포에서 추출된 확률변수와 관련된 불확실성 혹은 예측 불가능성의 척도로 해석할 수 있습니다. 또한, 엔트로피를 데이터 원천의 정보량을 정의하는 데도 활용할 수 있습니다. 예를 들어, 분포 $p$로부터 생성된 기호들의 나열 $X_{n} \sim p$를 관측되었다고 가정하겠습니다. 만약, $p$가 높은 엔트로피를 가진다면 각 관측값 $X_{n}$을 예측하기 어려울 것 입니다. 따라서, 데이터셋 $\mathcal{D} = \{ X_{1}, \dots, X_{n} \}$은 높은 정보량을 가진다고 이해할 수 있죠. 반대로 $p$가 아예 엔트로피가 0이라면 모든 $X_{n}$는 동일한 샘플을 얻게 됩니다. 따라서, 데이터셋 $\mathcal{D}$는 정보량이 많지 않습니다.
분포 $p$를 가지는 $K$개의 상태 위의 이산 확률변수 $X$의 엔트로피는 다음과 같이 정의할 수 있습니다.
$$\mathbb{H}(X) = -\sum_{k = 1}^{K} p(X = k) \log_{2}p(X = k) = -\mathbb{E}_{X}[\log p(X)] $$
여기서 $\mathbb{H}(X)$는 확률변수 $X$의 분포 $p$에 대한 엔트로피를 의미합니다. 아니면 명시적으로 $\mathbb{H}(p)$로 쓰는 것도 가능합니다. 이때, 단위는 비트(binary digit; bit)를 사용합니다. 예를 들어, $X \in \{ 1, \dots, 5 \}$고 분포가 $p = \{ 0.25, 0.25, 0.2, 0.15, 0.15 \}$라면 엔트로피는 2.29 비트가 됩니다. 만약, 로그의 밑을 자연상수 $e$를 사용한다면 단위는 nat이 됩니다.
엔트로피가 최대가 되는 경우는 균등분포입니다. 어떤 샘플이 나올 지 전혀 예측할 수 없기 때문이죠. 따라서, $K$개의 값을 가지는 확률 변수의 경우 $p(x = k) = \frac{1}{K}$일 때 엔트로피가 최대가 되며 이 경우 $\mathbb{H}(X) = -\sum_{k = 1}^{K} \frac{1}{K} \log (\frac{1}{K}) = -\log (\frac{1}{K}) = \log (K)$가 됩니다. 반대로 엔트로피가 0인 분포는 모든 확률 질량이 하나의 상태에만 두는 델타 함수 분포인 경우입니다. 이러한 분포에는 불확실성이 존재하지 않죠.
특수한 경우로 이항 확률변수 $X \in \{ 0, 1 \}$의 경우를 생각해보겠습니다. 여기서 $p(X = 1) = \theta$ 그리고 $p(X = 0) = 1 - \theta$라고 두면 엔트로피는 다음과 같이 쓸 수 있습니다.
$$\begin{align} \mathbb{H}(X) &= -[p(X = 1)\log_{2} p(X = 1) + p(X = 0)\log_{2} p(X = 0)] \\ &= - [\theta \log_{2} \theta + (1 - \theta) \log_{2} (1 - \theta)] \end{align}$$
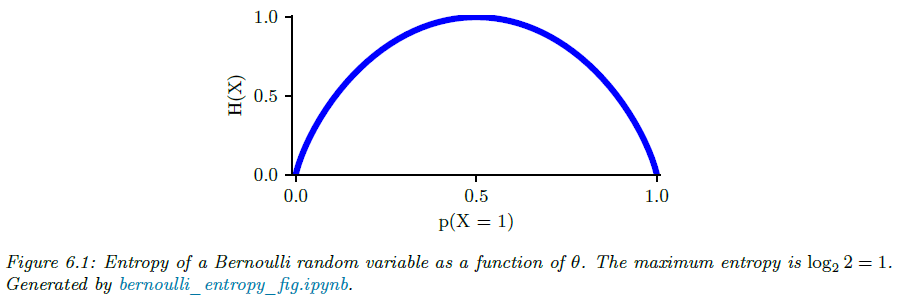
이를 이항 엔트로피 함수(binary entropy function)이라고 하면 $\mathbb{H}(\theta)$라고 표기합니다. 그림 6.1이 이 예시이며 분포가 균등한 $\theta = 0.5$에서 엔트로피가 최대값인 1비트를 가집니다.
2. DNA 서열 로고(DNA sequence logos)
엔트로피의 흥미로운 응용으로, DNA 서열 모티프를 표현하는 문제를 생각해 보도록 하겠습니다. 이는 짧은 DNA 문자열에 대한 분포입니다. 저희는 DNA 서열 집합을 정렬한 뒤 각 서열의 위치 $t$에서 알파벳 $\{ A, C, G, T \}$에 속하는 각 뉴클레오타이드의 경험적 분포를 추정할 수 있습니다. 이는 다음과 같이 정의됩니다.
$$N_{t} = \left( \sum_{i = 1}^{N} \mathbb{I}(X_{ii} = A), \sum_{i = 1}^{N} \mathbb{I}(X_{ii} = C), \sum_{i = 1}^{N} \mathbb{I}(X_{ii} = G), \sum_{i = 1}^{N} \mathbb{I}(X_{ii} = T) \right)$$
여기서 $N_{t}$는 특정 위치에서 각 무자가 나타난 횟수를 세는 길이 4의 벡터이고 $\hat{\theta}_{t} = \frac{N_{t}}{N}$ 분포를 위치 가중치 행렬(position weight matrix) 또는 서열 모티프(sequence motif)라 부릅니다.

그림 6.2는 이를 시각화한 결과입니다. (a)는 DNA 염기 서열이고 (b)는 위치 $t$에서 문자 $k$의 크기를 경험적 빈도 $\theta_{tk}$에 비례하게 그린 것 입니다. 또 다른 시각화 방식으로 서열 로고(sequence logo)가 있으며 이는 그림 (c)에서 보이는 것과 같D이 그릴 수 있습니다. 각 열은 $R_{t} = 2 - H_{t}$로 스케일링됩니다. 여기서 $H_{t}$는 $\hat{\theta}_{t}$의 엔트로피이며 $2 = \log_{2}(4)$는 4개의 문자에 대한 분포에서 가능한 최대 엔트로피를 의미합니다. 따라서, 엔트로피가 0인 분포는 높이가 2가 됩니다.
또한 불확실성과 관계없이 각 위치에서 가장 확률이 높은 문자를 단순히 계산할 수도 있는데, 이를 컨센서스 서열(consensus sequence)이라 한다.
3. 엔트로피 추정(Estimating Entropy)
많은 가능한 상태를 가진 확률변수의 엔트로피를 추정하기 위해서는 그 분포를 추정해야하고 이는 많은 데이터가 요구됩니다. 예를 들어 $X$가 영어 문서에서 단어의 정체성을 나타낸다고 가정하겠습니다. 드문 단어들이 긴 꼬리를 형성하고 새로운 단어들이 계속 만들어지기 때문에 $p(X)$와 따라서 $\mathbb{H}(X)$를 신뢰성 있게 추정하는 것은 어려울 수 있습니다. 이 문제에 관한 해결책은 향후에 더 자세히 알아보도록 하겠습니다.
