1. 정의(Definition)
저희는 MLE를 보다 일반적인 형태로 더 확장할 수 있습니다. MLE는 기본적으로 NLL을 최소화하는 $\theta$를 찾는 것으로 아래의 식에 대한 최적화를 수행합니다.
$$l(y_{n}, \theta; x_{n}) = -\log p(y_{n} \mid x_{n}, \theta)$$
하지만, 반드시 로그 손실만 써야하는 법은 없습니다. 로그 손실대신 임의의 손실함수 $l(\cdot)$을 넣어도 동일한 틀은 유지하면서 다른 방식으로 최적화를 수행할 수 있습니다. 이렇게 하면 다음과 같이 경험적 위험(Empirical Risk)를 최소화하는 문제를 일반화할 수 있습니다.
$$\mathcal{L}(\theta) = \frac{1}{N} \sum_{n = 1}^{N} l(y_{n}, \theta; x_{n})$$
이러한 방식을 경험적 위험 최소화(Empirical Risk Minimization; ERM)이라고 합니다. 이 부분에 대한 내용은 향후에 더 자세히 알아보도록 하겠습니다. 대신, 왜 "경험적"이라고 부를까요? 기댓값 관점에서 보면, 우리는 진짜(잠재적) 데이터 분포가 아니라 학습 데이터가 만들어 내는 경험적 분포(모집단의 표본 분포) 위에서 손실의 평균을 계산하고 있습니다. 따라서, ERM은 “경험적” 데이터 분포에 대한 기대 손실이기 때문에 경험적이라고 부르게 되는 것이죠. 이제 몇 가지 중요한 예시를 보도록 하겠습니다.
2. 오분류율 최소화(Minimizing the Misclassification Rate)
분류 문제를 풀 때는 0-1 손실(0-1 loss)를 사용해볼 수 있습니다. 0-1 손실은 예측이 맞으면 0, 틀리면 1을 부여하는 가장 단순한 형태의 오류 측정 방식으로 다음과 같이 정의할 수 있습니다.
$$\begin{equation}
\ell_{01}(y_n,\theta; x_n)=
\begin{cases}
0 & \text{if } y_n = f(x_n;\theta),\\[4pt]
1 & \text{if } y_n \neq f(x_n;\theta).
\end{cases}
\end{equation}$$
여기서 $f(x; \theta)$는 입력 $x$에 대해 매개변수 $\theta$를 가진 모델이 내놓은 예측값을 의미합니다. 이를 기반으로 ERM을 수행하기 위해서는 다음과 같은 식을 최소화하면 됩니다.
$$\mathcal{L}(\theta) = \frac{1}{N} \sum_{n = 1}^{N} l_{01}(y_{n}, \theta; x_{n})$$
즉, 위 식은 훈련 집합 $\mathcal{D}$에서의 평균 오분류율이라고 볼 수 있습니다. 이는 $\theta$라는 파라미터를 가지는 모델이 훈련 데이터 $N$개를 얼마나 자주 틀렸는지를 직접 계산해보는 것과 동일합니다.
만약, 풀려고 하는 문제가 이진 분류(Binary Classification)이라면 라벨을 $\{-1, +1\}$이라고 두면 더 깔끔하게 표현할 수 있습니다. 여기서 $\tilde{y} \in \{ -1, +1 \}$을 참값, 그리고 $\hat{y} = f(x; \theta) = \{ -1, +1 \}$을 모델의 예측값이라고 두겠습니다. 0‑1 손실을 지시 함수로 표현하면 다음과 같습니다.
$$l_{01}(\tilde{y}, \hat{y}) = \mathbb{I}(\tilde{y} \neq \hat{y}) = \mathbb{I}(\tilde{y}\hat{y} < 0)$$
이때, $\tilde{y}\hat{y} < 0$라는 것은 참값과 예측값의 부호가 다르다는 것을 의미하기 때문에 잘못된 예측을 수행했음을 의미합니다. 최종적으로 경험적 위험은 다음과 같이 표현할 수 있습니다.
$$\mathcal{L}(\theta) = \frac{1}{N} \sum_{n = 1}^{N} l_{01}(y_{n}, \theta; x_{n}) = \frac{1}{N} \sum_{n = 1}^{N} \mathbb{I}(\tilde{y}_{n}\hat{y}_{n} < 0)$$
3. 대체 손실(Surrogate Loss)
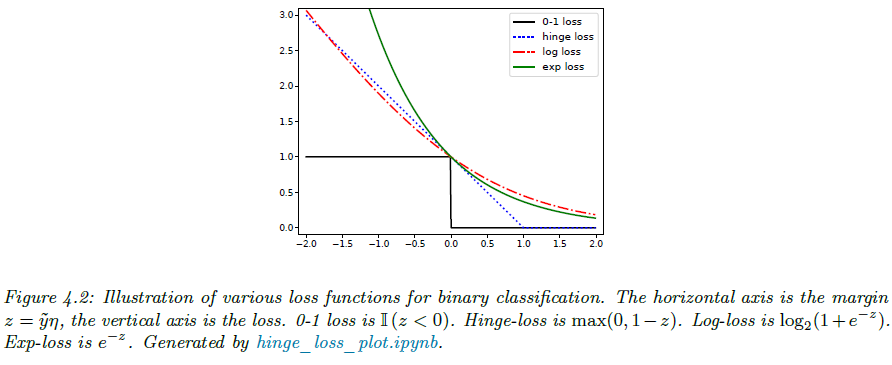
하지만 방금 보았던 0-1 손실의 경우 계단함수이기 때문에 그림 4.2에서 볼 수 있다싶이 매끄럽지 않습니다. 이로 인해 최적화가 매우 까다롭고 실제로는 NP-Hard 문제로 알려져 있습니다. 그래서 실무에서는 보통 다른 손실함수를 사용합니다. 핵심적인 아이디어는 1) 0-1 손실을 직접 최소화하기보다 2) 볼록 상계(Convex Upper Bound)를 가지는 손실함수를 만들고 3) 이 손실함수를 최소화하면 계산이 훨씬 간단해집니다.
가장 대표적으로 쓰이는 손실함수가 바로 로그 손실입니다. 이진 확률 분류기는 라벨 분포를 다음과 같이 변환시키게 됩니다.
$$p(\tilde{y} \mid x, \theta) = \sigma(\tilde{y}\eta) = \frac{1}{1 + e^{-\tilde{y}\eta}}$$
여기서 $\eta = f(x, \theta)$로 로짓을 의미합니다. 이에 대응되는 로그 손실은 다음과 같습니다.
$$l_{\text{ll}}(\tilde{y}, \eta) = -\log p(\tilde{y} \mid \eta) = \log (1 + e^{-\tilde{y}\eta})$$
이때, $\tilde{y}\eta$는 ‘마진(margin)’으로 값이 0이면 결정 경계에 딱 걸친 상태를 의미하고 값이 양수로 클수록 “안전 여유(margin of safety)”가 커지게 됩니다. 그림 4.2를 보면, 로그 손실은 0‑1 손실 위를 부드럽게 감싸는 볼록 상계임을 알 수 있습니다. 즉 음의 로그 가능도(negative log‑likelihood) 를 최소화하는 일은 경험적 0‑1 손실의 꽤 촘촘한 상계를 최소화하는 것과 동치입니다.
다음으로 0‑1 손실에 대한 또 다른 볼록 상계가 힌지 손실입니다.
$$l_{\text{hinge}}(\tilde{y}, \eta) = \text{max} (0, 1 - \tilde{y}\eta) = (1 - \tilde{y}\eta)_{+}$$
그림 4.2에서 보듯, 문 경첩(hinge)처럼 한쪽만 열려 있는 모양입니다. 이 함수는 볼록(convex) 하지만 전체적으로 매끄럽진 않고 구간별(조각별)로만 미분 가능합니다.
